etcd存储引擎之b+树实现
0 前言
本期我们继续延续 etcd 存储引擎系列的话题. 在该系列中,我们以 boltdb 作为 b+树 工程化落地的学习案例,该项目开源地址为:https://github.com/etcd-io/bbolt,go 语言纯度接近 100%. (本系列涉及走读的 boltdb 源码版本为 v1.3.8)
下面是本专题的分享节奏,本文是其中的第三篇——b+树实现篇:
- etcd存储引擎之主干框架(已完成):偏宏观视角下介绍 boltdb 的定位、架构、特性,通过几个核心流程浅探 boltdb 实现源码
- • etcd存储引擎之存储设计(已完成):介绍 boltdb 存储模型、机制的设计实现,包含磁盘、内存两部分
- etcd存储引擎之b+树实现(本篇):介绍 b+ 树理论模型及 boltdb 实现案例,包括模型定义及 crud 流程梳理
- etcd存储引擎之事务实现(待填坑):介绍 boltdb 事务的执行模式及实现原理
1 理论模型
本文我们聚焦于 boltdb 针对 b+ 树的技术实现细节,b+ 树是 b 树的迭代升级版本,因此,我们有必要先理清楚关于b树和b+树的理论模型和核心性质.
1.1 b树
1.1.1 用途
首先,我们需要对计算机存储模型有个基本的概念认知. 常用的计算机存储介质分为内存 memory (全称 main memory) 和磁盘 disk (又称外存 external memory):
- 内存速度快,但价格昂贵,容量有限(好钢用在刀刃上),且具属于数据易失性存储介质(设备断电时,数据会丢失).
- 磁盘速度慢,但价格便宜,容量充足,且能保证数据持久化稳定存储.
从性能层面,我们补充一些定量描述:访问一次内存的耗时大约为 100 ns 的量级,而访问一次磁盘的耗时可能处在 10 ms 的量级,两者之间的速度差距达到 10万倍.
举个更生动的例子来反映两者的效率差距——倘若访问一次内存的耗时是 1 秒,那么访问一次磁盘的耗时约为 1.2 天左右.
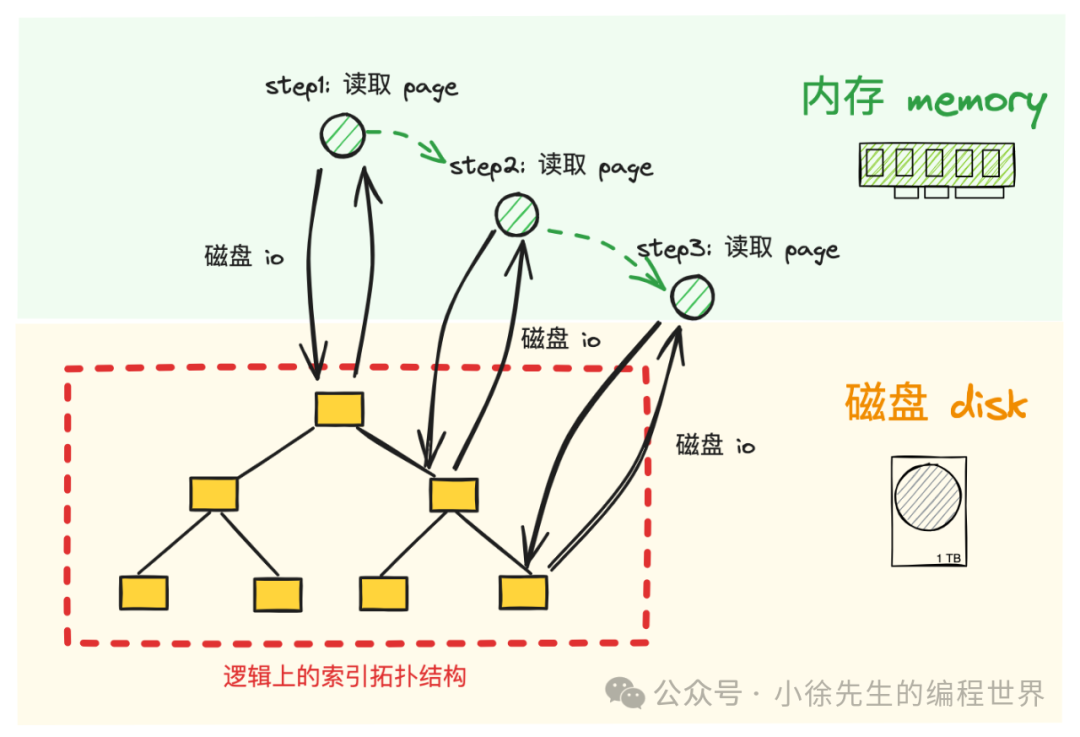
针对于数据库系统的设计来说,通常宁可接受访问内存 100次也要避免访问磁盘 1 次. 因此,提升性能的关键点很大程度上在于如何减少访问磁盘的 io 次数,而不在于如何提效磁盘访问行为本身. 这个过程中也需要结合局部性原理的应用,尽可能把需要用到的热数据缓存在内存中加以复用.
在这样的前提之下,类似 b 树这样的多叉搜索树数据结构,是很适用于作为读密集型数据库或文件系统的索引模型的. 虽然在写流程中,涉及到对索引结构的调整存在一定的代价,但是在读流程中,每与索引的一次交互对应一次磁盘 io,检索进度也会因此向下递进一层,最坏的情况下在来到叶子节点时也必然会得到检索结果. 由于 b 树形状扁平,高度很低,因此对应的磁盘 io 次数也会很少.
1.1.2 定义
下面我们捋一下有关于 b 树的定义.
b 树,英文名为 b-tree,因此很多人也把其称为 b-(jiǎn)树,但大家需要明白,其实说的是同一个东西. b 树是一种自平衡的多叉搜索树,通过维护有序的数据结构,保证能够基于对数级别的时间复杂度完成搜索、插入和删除操作.
下面是详细定义:
b 树是一种平衡多叉搜索树,伴随着每个 b 树实例都有一个阶数的概念,针对于一棵 n 阶 b 树,需要满足:
- 所有叶子节点处在相同的层级,即从根节点出发到底端的各条路径高度一致
- 每个父节点最多只有 n 个子节点,且父节点内元素个数为子节点数 - 1
- 除了根节点外的父节点,至少拥有 [n/2] 个子节点("[]" 表示向上取整)
- 倘若根节点存在子节点,则至少拥有 2 个子节点
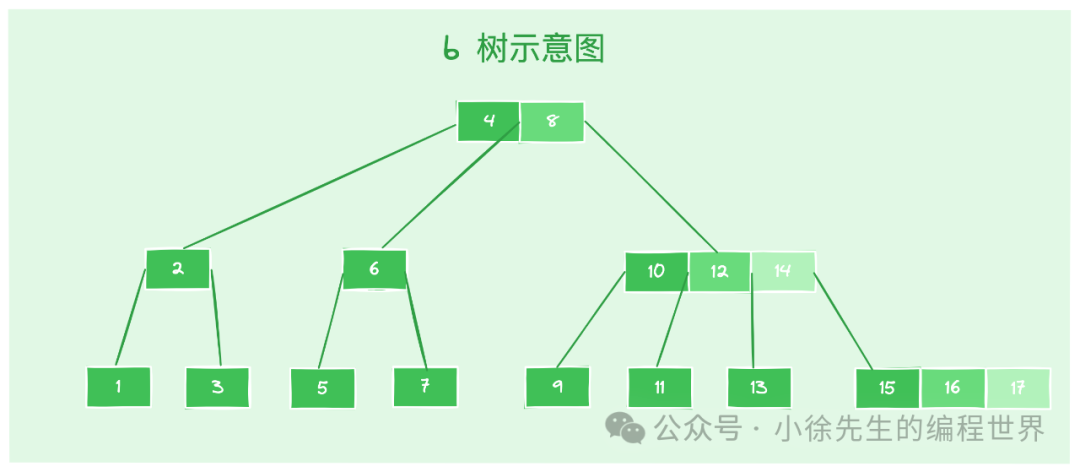
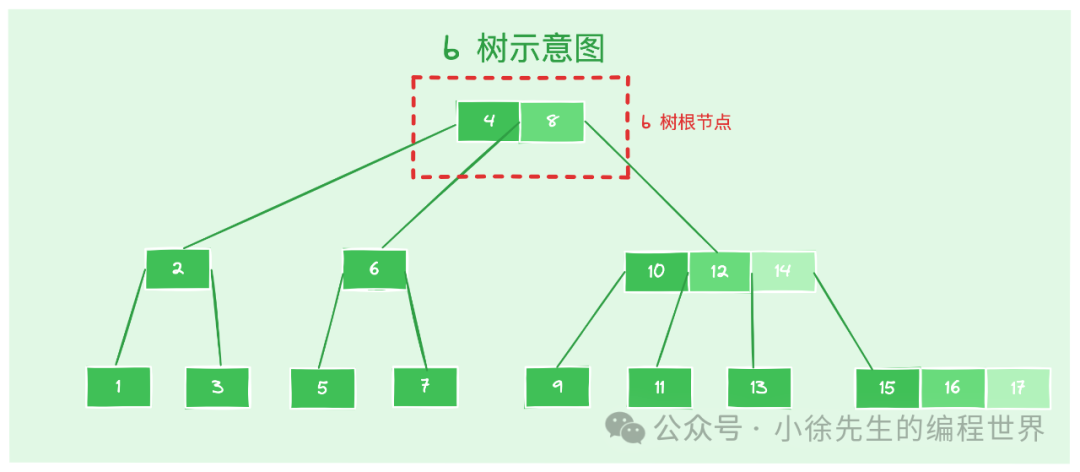
一棵 4 阶 b 树的示意图如下所示:
在基础定义之上,再针对其中涉及到的几个核心概念展开说明:
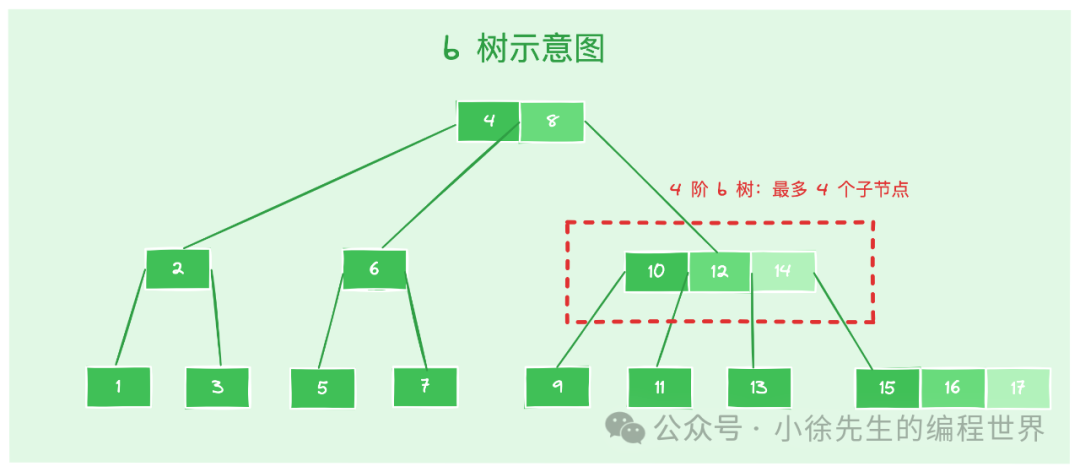
- 阶数 n:限定了 b 树中父节点的最大子节点个数,并限定了除根节点外,其它父节点的子节点个数的下限(>= [n/2]). 因此,阶数和 b 树的扁平化程度正相关,阶数越高,b 树横向拓展性越好,同等数据量下高度就越低,而单个节点内存储的数据量就越多.
通过下方的示意图能看到,【10,12,14】节点正好达到了阶数 4 的上限,其拥有的子节点数 量恰好为 4 个,如果再多的话就需要调整处理了.
- 根节点:b 树的起点,拥有的子节点数量上限同样受到阶数的限制 <= 阶数 n. 但根节点的子节点数量下限比较特殊:
- 如果根节点同时为叶子节点,则子节点数可以为 0,此时整棵 b 树只有一个节点
- 如果根节点拥有子节点数,那么子节点个数至少为 2
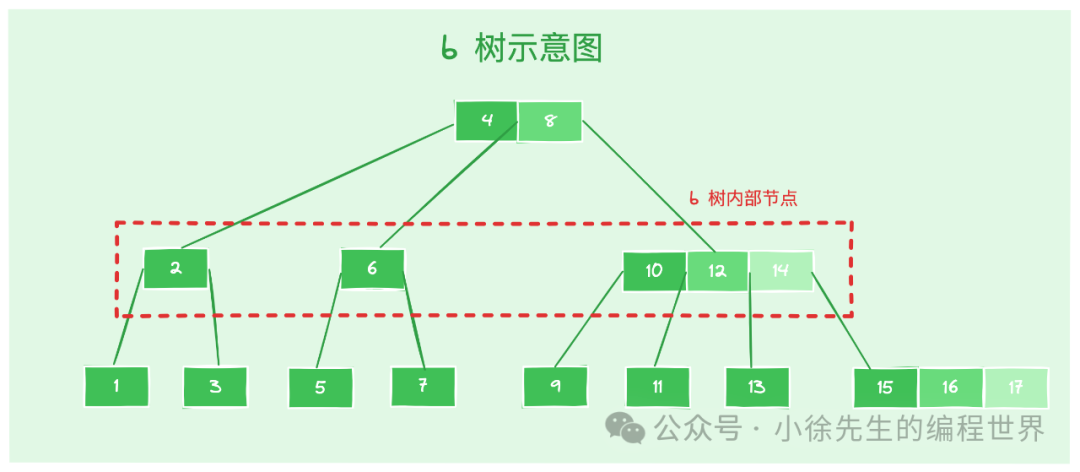
- 内部节点:除根节点外拥有子节点的父节点. 拥有的子节点数量上限同样受到阶数的 <= 阶数 n,且拥有子节点的数量 >= [n/2] ("[]" 表示向上取整). 又由于父节点 key 个数为子节点树 - 1,因此可以总结如下:
- 内部节点的子节点数量 x 满足: [n/2] <= x <= n
- 内部节点的元素数量 x 满足:[n/2] - 1 <= x <= n - 1
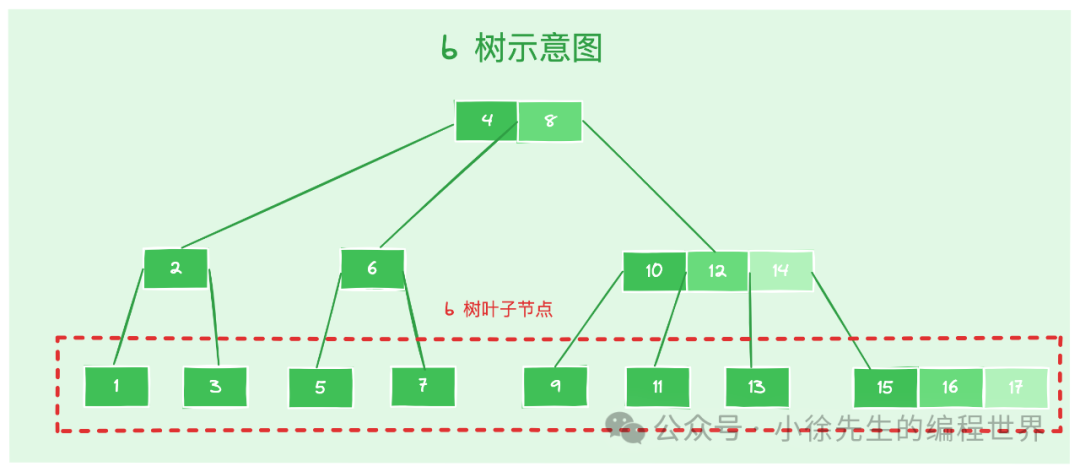
- 叶子节点:不存在子节点的最底层节点,处于同一层级. 叶子节点的元素数量限制为:
- 叶子节点子节点数量 x 满足:x = 0
- 叶子节点元素数量 x 满足:[n/2] - 1 <= x <= n - 1
下面给大家提供一个可用于可视化动态展示 b 树构造进程的网站,传送门如下:
b 树可视化—— https://www.cs.usfca.edu/~galles/visualization/BTree.html
1.1.3 示例
为了帮助大家进一步加深对 b 树的理解,下面给出几个详细的操作案例加以说明:
首先针对 b 树的元素插入流程,核心步骤如下:
- step1:根据元素找到其应该从属的叶子节点
- step2:在叶子节点合适位置中插入元素
- step3:倘若插入后叶子元素数量 <= 阶数 n,直接结束流程
- step4:倘若插入后叶子元素数量 > 阶数 n,则沿中间元素将节点分裂两个节点,并将中间节点上升插入到父节点中
上述 step4 的步骤称之为 “spill”,它可能进一步引起父节点元素数量超限,因此会针对父节点递归执行 step4. 最坏的情况下,可能一直分裂到根节点,最终生成新的根节点实例,导致 b 树整体高度加 1.
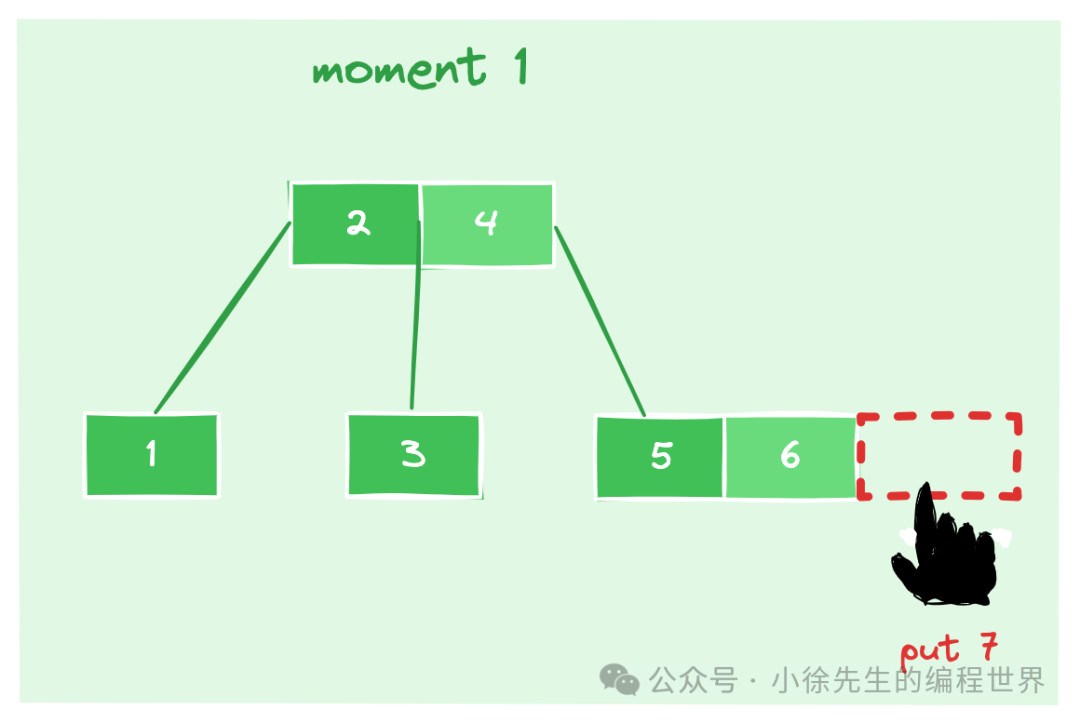
下面是针对一棵 3 阶 b 树的元素插入案例:
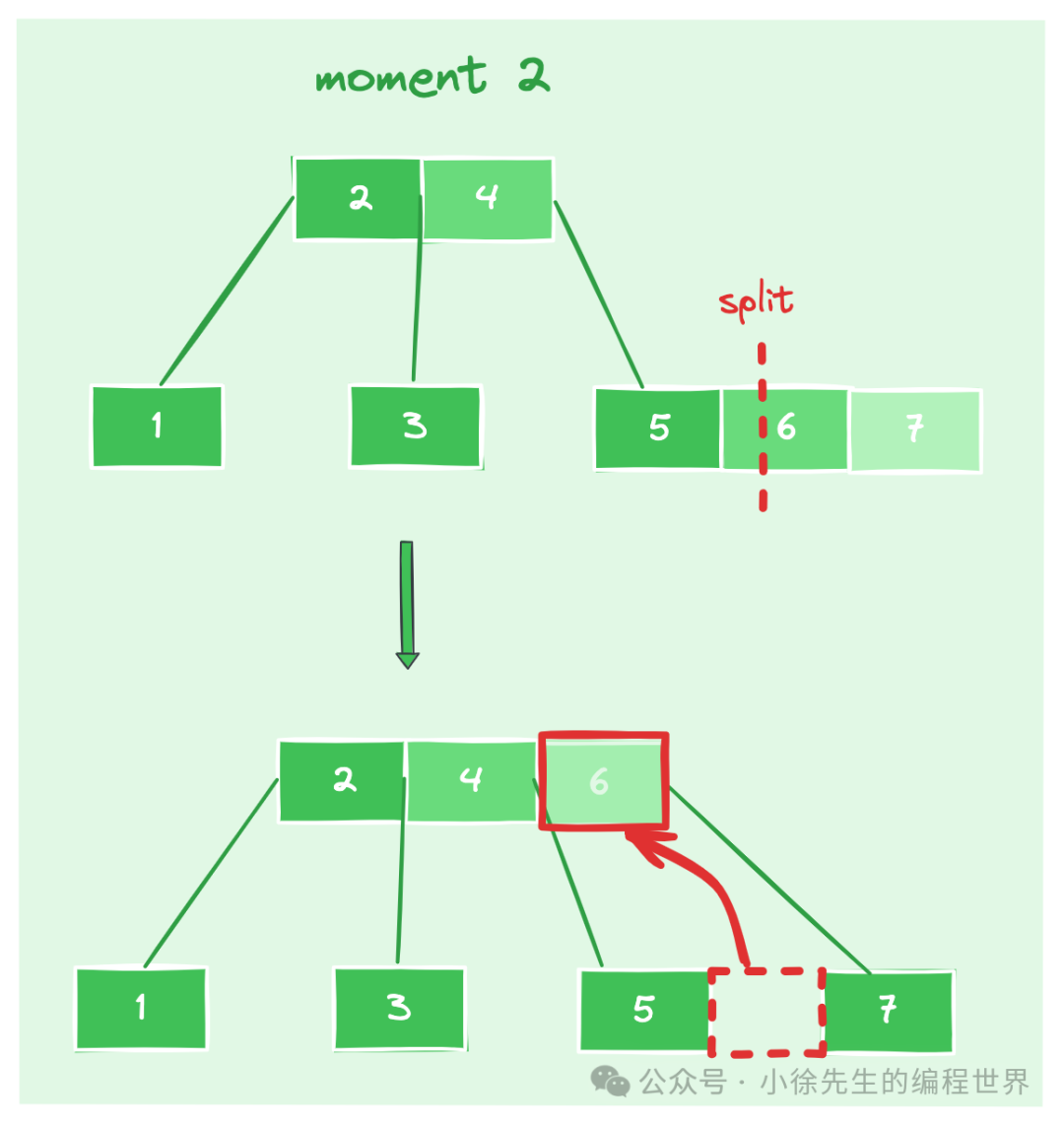
- moment1:原本 b 树中已存在元素【1,2,3,4,5,6】,此时拟在节点【5,6】中插入一个新的元素——7
- moment2:插入元素 7 后,节点【5,6,7】元素数量 > 阶数 - 1,因此沿中间元素 6 进行 split,拆分成 【5】和 【7】两个独立节点,并把元素 6 追加到父节点中,形成新的父节点结构:【2,4,6】
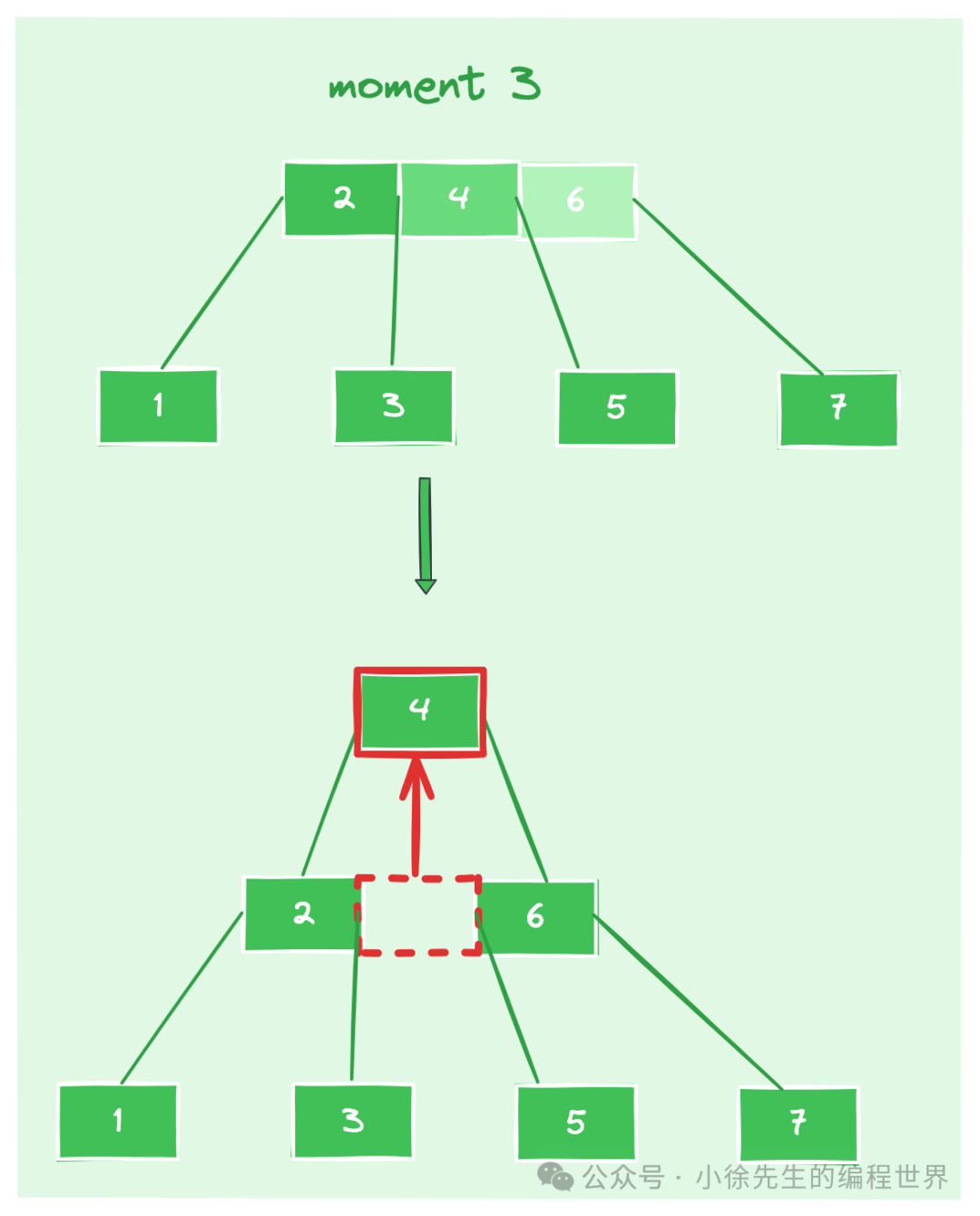
- moment3:此时父节点【2,4,6】的元素数量 > 阶数 - 1,因此沿中间元素 4 进行 split,拆分成 【2】和 【6】两个独立节点,并对元素 4 进行上升,因为不存在父节点,因此构造出一个新的父节点【4】,至此,spill 流程结束,整棵 b 树高度加 1
下面针对 b 树的元素删除流程进行梳理,这一块儿相对复杂一些,核心步骤如下:
- step1:根据元素找到从属的叶子节点
- step2:在叶子节点中删除对应元素
- step3:如果被删除数据是处在某个父节点中的索引结构,其原本关联了左右子节点,则转移其中一个子节点中最相近的元素到父节点被删除元素的位置;如果没有左右子节点,则忽略本步骤
- step4:查看此时是否存在节点,元素数量不满足 >= [n/2] - 1 的条件. 如果没有,则结束流程,否则需要先查看其相邻兄弟节点的数据状况
- step5:如果有相邻兄弟节点比较丰满(数据条数 > [n/2] - 1),则向父节点借一个最相近的元素填补被删除元素所在位置,再从丰满兄弟节点处借一笔相近数据填充到父节点被借走元素的所在位置
- step6:如果相邻兄弟节点都比较消瘦(数据条数 <= [n/2] - 1),则和相邻兄弟节点以及父节点被覆盖到的局部元素 "合并" 成一个新的节点.
step4-step6 的流程称之为“rebalance”. 如果执行到 step6 ,则需要检查父节点状况是否满足条件,如果不满足,则以父节点为起点沿 step4 开始递归执行. 最不利的情况可能层层向上递归合并,最终 b 树的整体高度可能会下降.
下面是针对一棵 5 阶 b 树的元素删除案例:
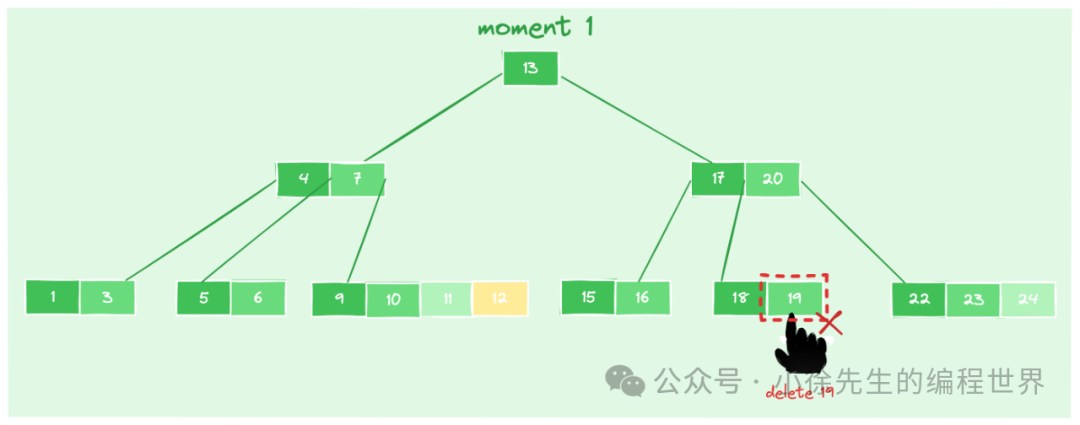
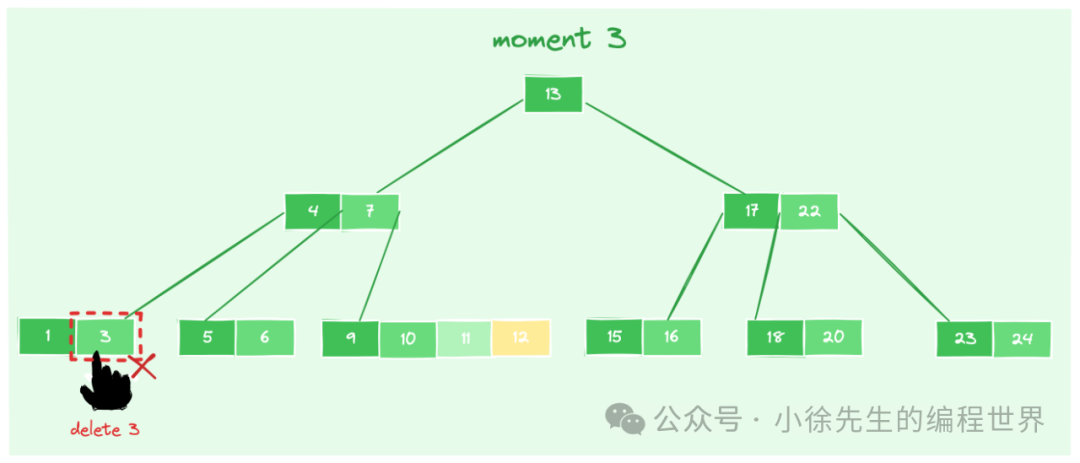
- moment1:原本 b 树中已存在元素【1,3,4,5,6,7,9,10,11,12,13,15,16,17,18,19,20,22,23,24】,此时拟在节点【18,19】中删除元素——19
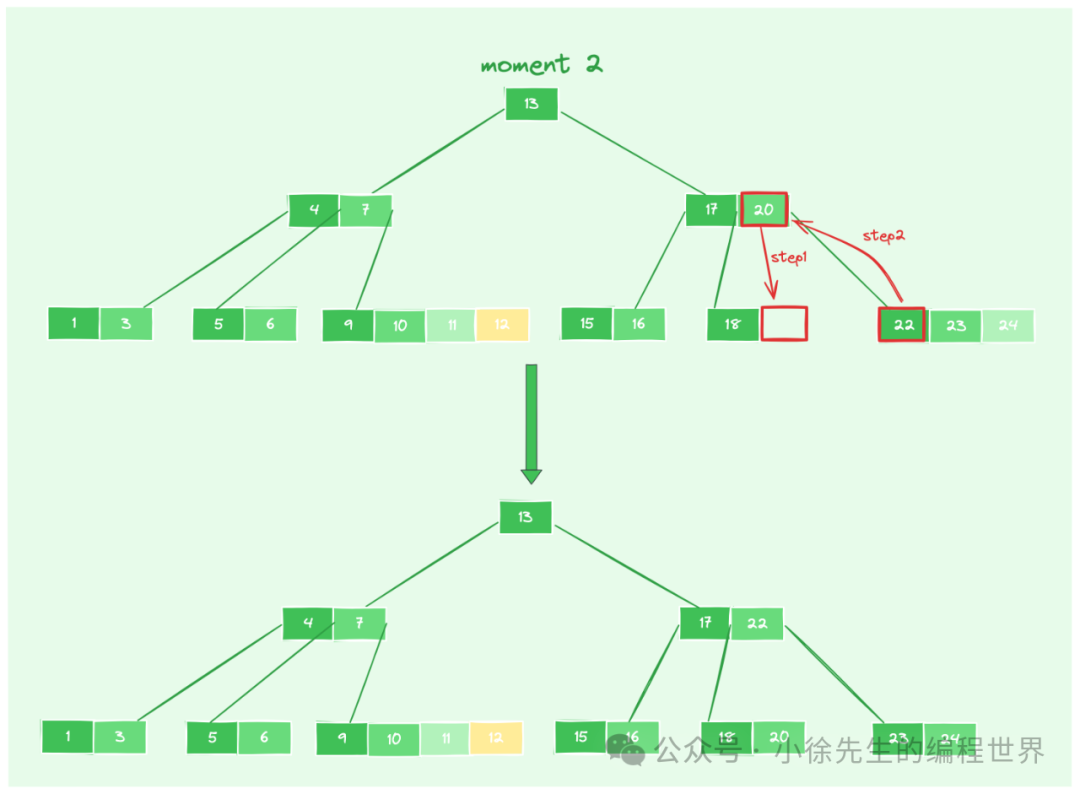
- moment2:删除 19 后,节点【18】不满足 >= [n/2] - 1 的数量下限,于是查看相邻兄弟节点的数据状况,发现兄弟节点【22,23,24】比较丰满,数据量 > [n/2] - 1. 接下来,从父节点中借来元素 20,节点【18】-> 【18,20】,满足数量下限,再从兄弟节点中借来元素 22,父节点【17,20】-> 【17,22】. 至此,一轮 rebalance 流程结束,所有节点数据均满足条件.
- moment3:在 moment2 的基础上,进一步尝试从节点【1,3】中删除元素 3
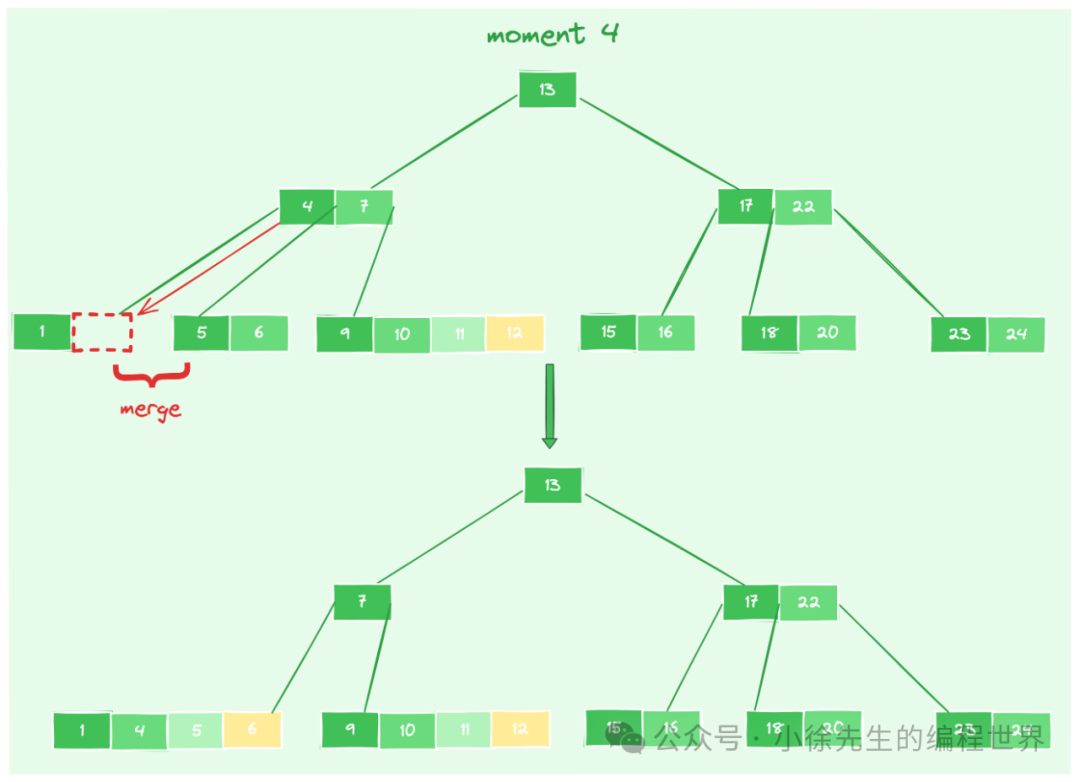
- moment4:删除 3 后,节点【1】不满足 >= [n/2] - 1 的数量下限,紧接着查看相邻兄弟节点的数据状况,发现没有丰满的兄弟节点. 于是节点【1】、消瘦兄弟节点【5,6】以及父节点局部数据范围【4】进行合并,生成新节点【1,4,5,6】
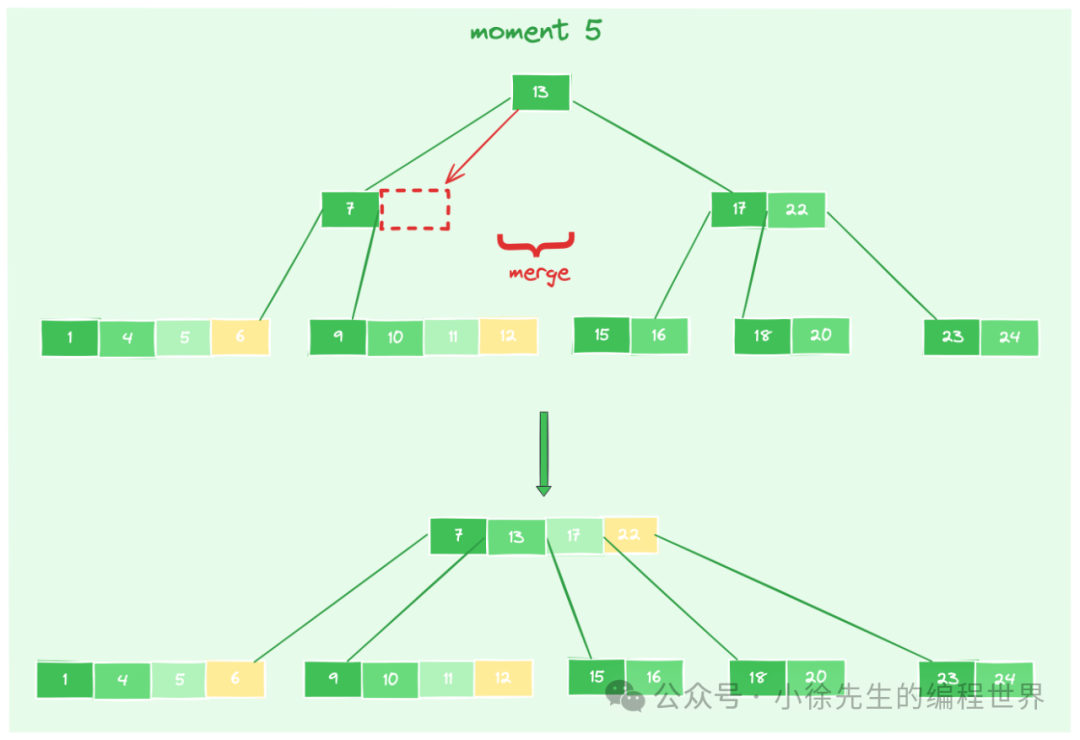
- moment5:然而新的问题出现了,子节点合并后,父节点【7】不满足 >= [n/2] - 1 的数量下限,查看相邻兄弟节点【17,22】发现也是消瘦的类型,于是重复合并规则,将子节点【7】、兄弟节点【17,22】和父节点【13】合并到一起,形成一个新节点【7,13,17,22】. 至此 reblance 流程结束,b 树整体高度减 1
相信通过上面补充的两个案例,大家对 b 树的特性和机制都有了进一步的认识,下面我们以 b 树为基础,展开关于 b+ 树的介绍.
1.2 b+树
1.2.1 定义
b+树继承了 b 树的绝大多数特性,并在基础上作了几点调整:
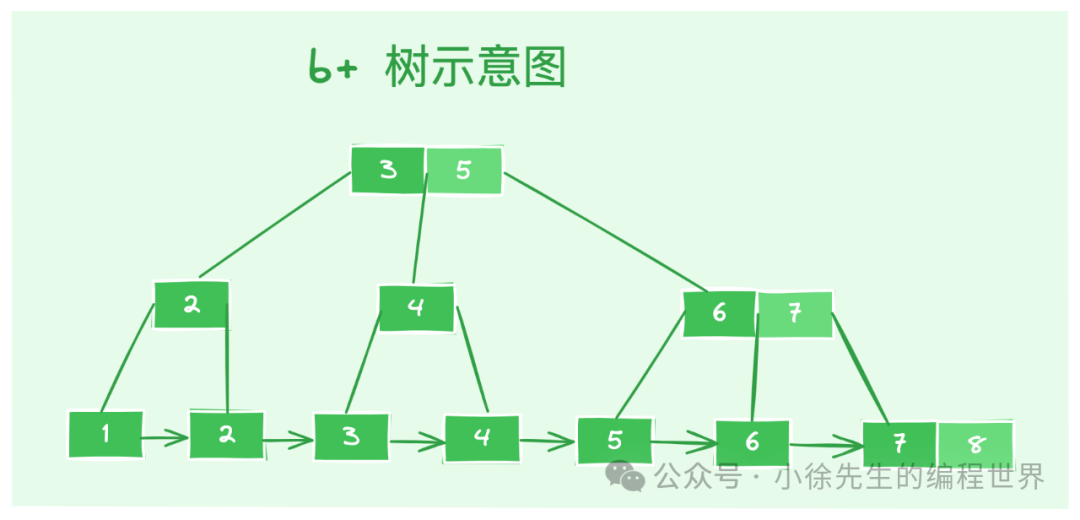
- 全量数据均存放于叶子节点,非叶子节点只作索引. 在父节点中,每处元素会冗余其右子树中的最小元素作为索引值
- 叶子节点彼此间通过指针串联形成有序的单向链表
下面给出一个 3 阶 b+ 树示意图,展示如下:
下面是个可用于可视化动态展示 b+ 树构造进程的网站,传送门如下:
b+ 树可视化—— https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html
1.2.2 对比b树
我们通常认为,b+ 树相比于 b 树更加适合于用于作为读密集型数据库的索引结构,其原因就在于:
- 更高效的性能: 正如 1.1.1 节我们所聊的,性能瓶颈取决于磁盘 io 的次数. 由于 b+ 树所有非叶子节点只存放索引信息,不存放实际数据,这使得相同的节点大小之下,能存放的索引信息更多,进一步使得 b+ 树相比于 b 树形状更扁平,高度更低,因此磁盘 io 次数更少,对应性能表现就更好
- 更稳定的性能: 因为 b+ 树全量数据存储于叶子节点,因此每次读流程都需要走到底部的叶子节点处,磁盘 io 次数固定,相对 b 树更加稳定
- 更适合范围检索: 因为 b+ 树全量数据存储于叶子节点,且建立成单向有序链表结构,因此更利于范围查询操作
至此,我们介绍完有关 b+ 树的理论部分,下面我们就一起进入到 boltdb 的源码中,探讨有关于 b+ 树的具体实现细节.
2 实现模型
2.1 实现差异点
有关于 b+ 树的定义是偏理论的,在真正付诸实践时,boltdb 作了如下几处调整:
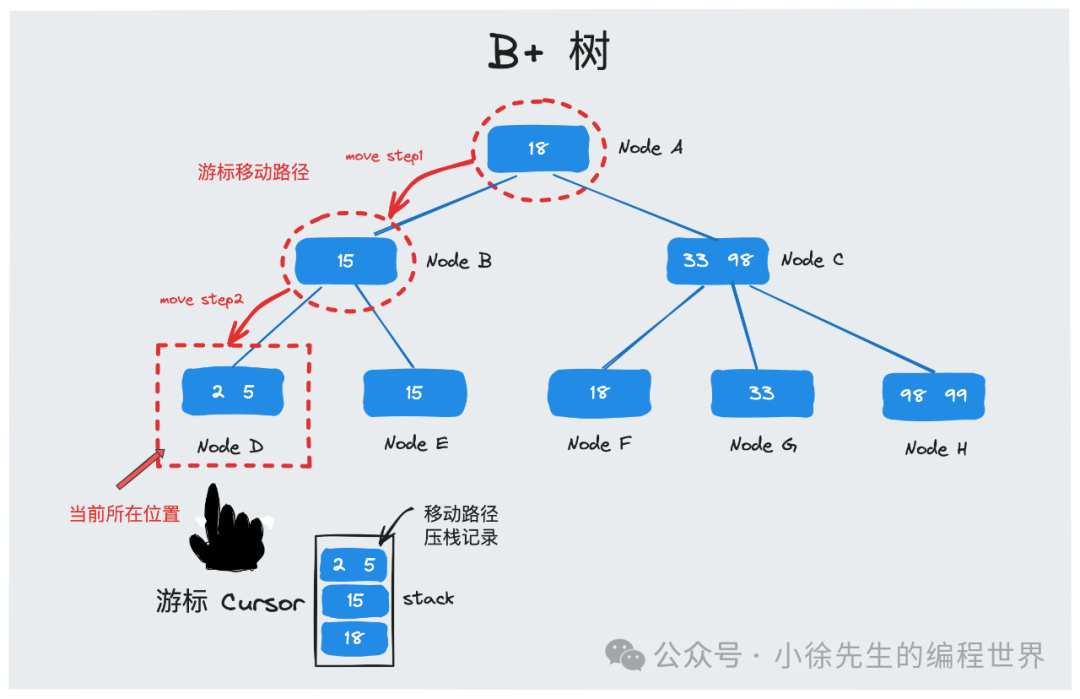
- 游标代替叶链表
为了降低模型复杂度,boltdb 没有将 b+ 树叶子节点通过单向指针串联成链,而是引入了一个游标结构,通过记录检索移动路径结合路径回溯的方式,来支持范围检索的诉求.
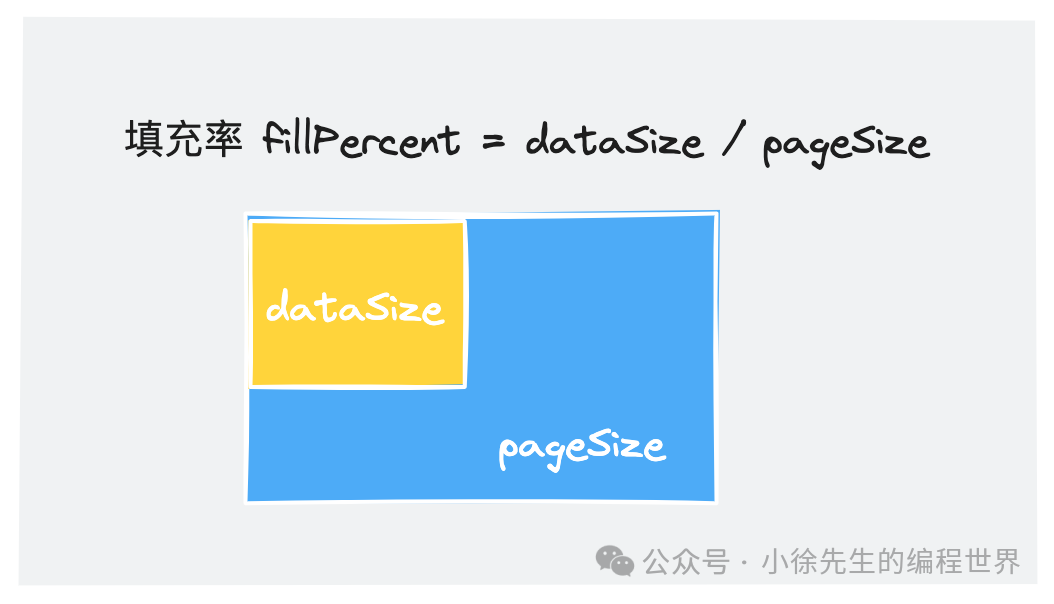
- 填充率代替阶数
由于 boltdb 中,kv 数据是不定长的,因此不适合通过阶数来限定节点容量. 这里采取的方式是启用了数据填充率(填充率 fillPercent = dataSize / pageSize) . 当某个节点数据填充率 <= 0.25 时,需要进行 rebalance,使节点变得更加丰满;当某个节点数据填充率大于用户设定的阈值时,需要进行 spill,需要保证拆分后的节点不能过于臃肿.
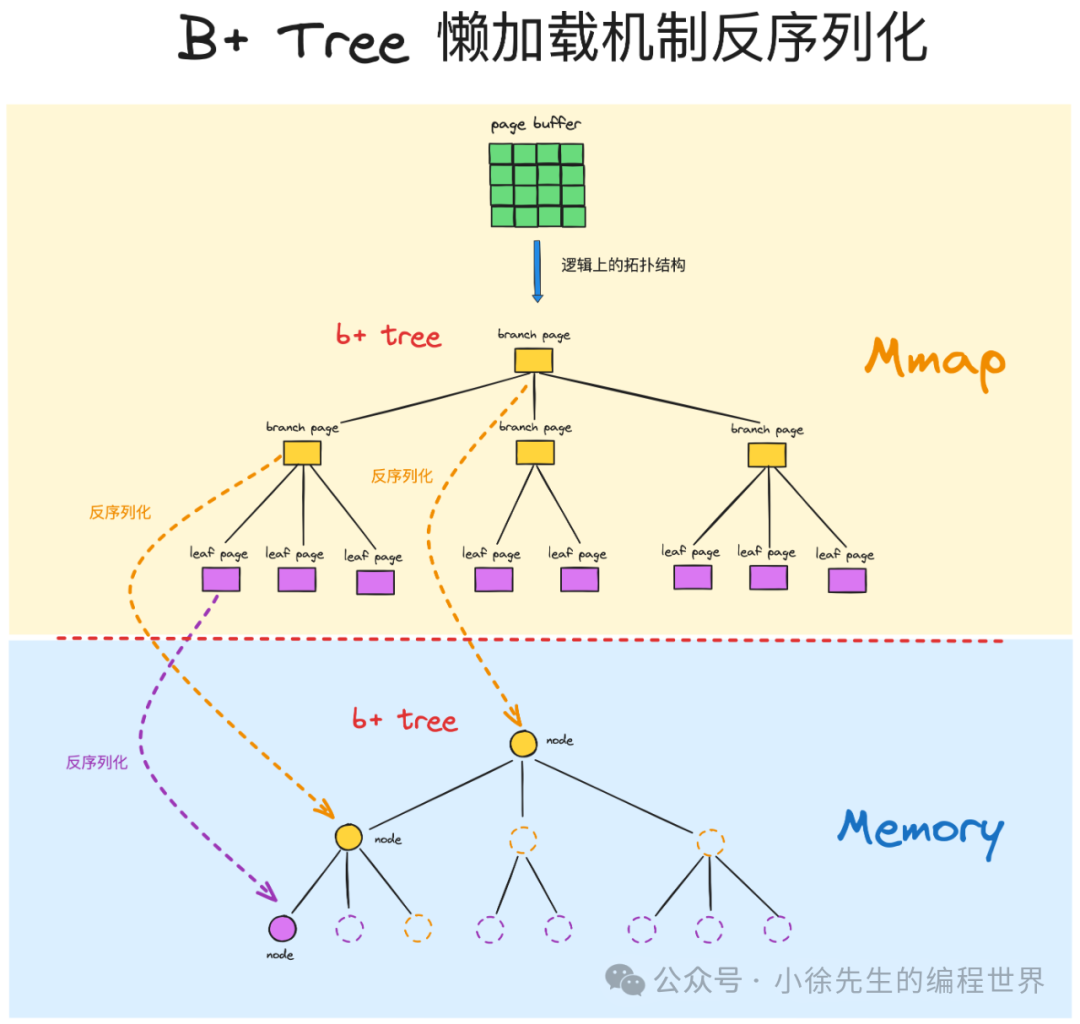
- “磁盘的树”与“内存的树”
boltdb 针对 b+ 树的实现根据存储介质可以分为磁盘与内存两个版本. 磁盘上的是持久化的 b+树,需要严格保证其平衡性,而内存中的是读写事务运行时使用的 b+ 树副本(copy-on-write),基于懒加载机制反序列得到,在运行过程中不会因为单笔改动而频繁执行 reblance 和 spill 操作,而是在事务提交时,一次性完成 b+ 树的自平衡调整操作,最后再将完整的内容持久化为稳定版本的“磁盘的树”.
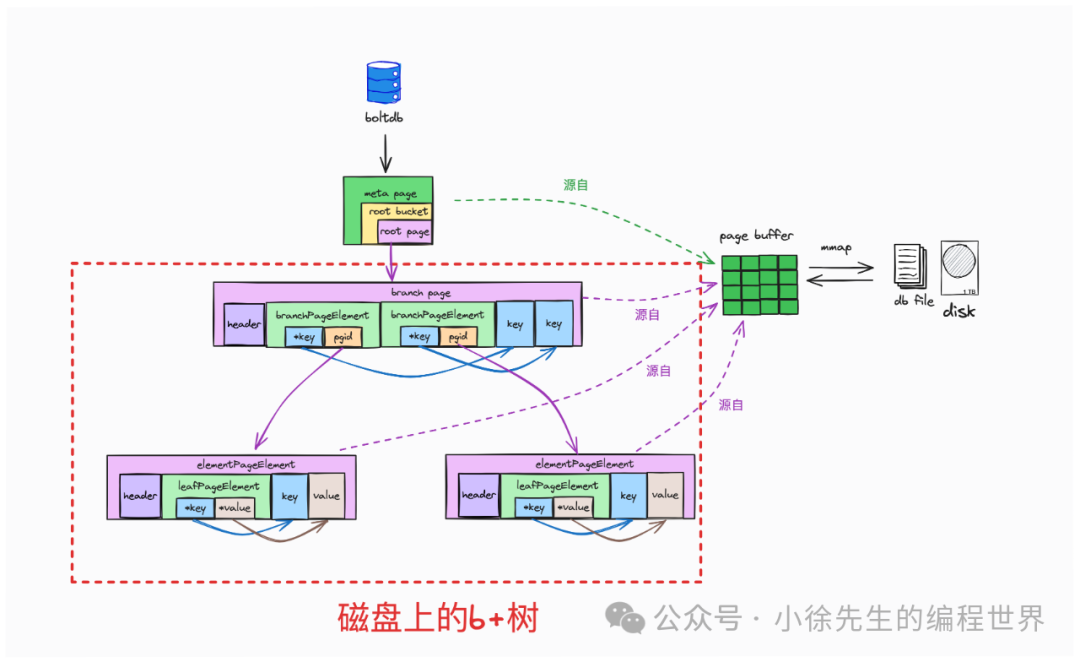
2.2 “磁盘中的树”
上图展示了磁盘上的 b+ 树的实现细节,一切的根源要从 db 实例的 meta page 中说起. 我们知道每个 db 实例会持有两个轮换使用的 meta page,代码如下:
// db 实例
type DB struct {
// ...
// 两个轮换使用的 meta page
meta0 *meta
meta1 *meta
// ...
}每个 meta page 对应数据的一个持久化版本,其中持有一个 root bucket:
type meta struct {
// ...
// 始祖 bucket
root bucket
// ...
}一个 bucket 对应一张表,其中通过 root 字段标识了表中 b+ 树根节点对应的 page id:
// bucket header,表示一张表
type bucket struct {
// b+ 树根节点 page id
root pgid
// ...
}通过 page id 可以得到每个 page 对应的 header,进一步可通过 ptr 取得 page body:
// page header,当 flags 为 branch 或 leaf 时,对应一个磁盘上的 b+ 树节点
type page struct {
id pgid // page id
flags uint16 // page 类型,b+ 树枝干节点对应为 branch;叶子节点对应为 leaf
count uint16 // page 内的数据量,对应 b+ 树节点表示节点内 key 的数量
ptr uintptr // page body 的起始位置
// ...
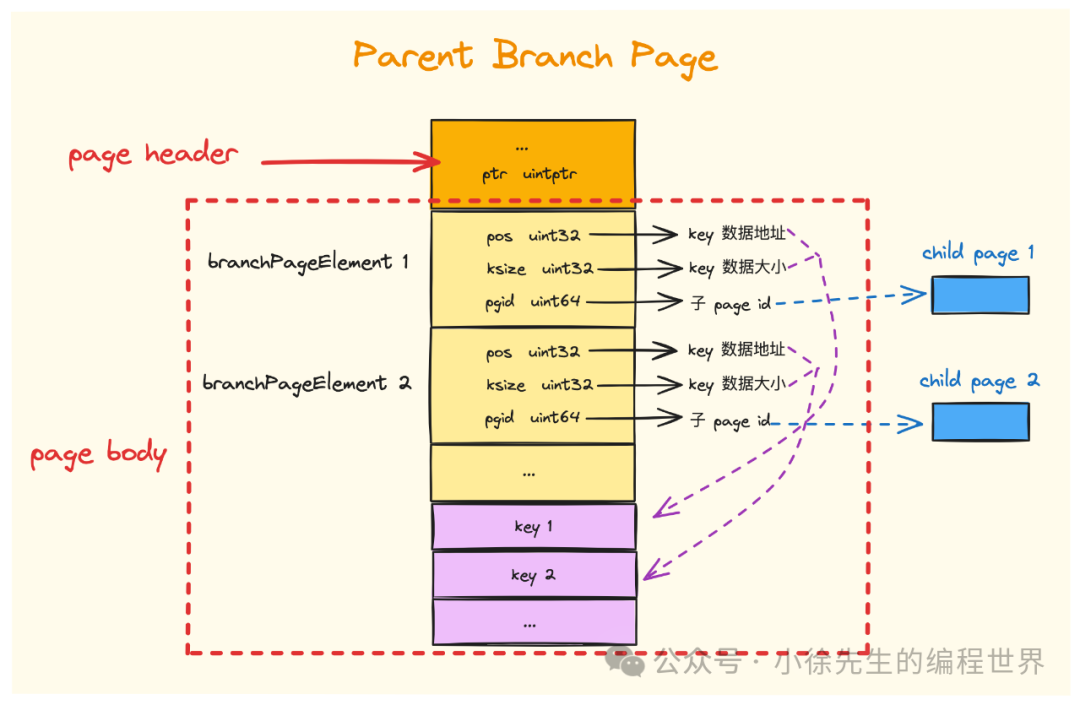
}b+ 树中的持久化节点分为 branch page(枝干节点)和 leaf page(叶子节点)两种类型,采用 shadow paging 技术标识每组元素的所在位置.
针对 branch page 的结构示意图如上,其中通过 branchPageElement 标识每个内部元素的信息,其中通过 pos 和 ksize 指向的 key 值就是枝干节点中的索引,pgid 就是指向子节点的指针:
// 在 branch page 中标识一组 key 的 header
type branchPageElement struct {
pos uint32 // key 的起始位置
ksize uint32 // key 的大小,单位 byte
pgid pgid // key 映射子节点的 page id
}从 branch page 的 header 出发,通过 index 可以获取到指定的 branchPageElement:
// 获取 branch page 中指定 index 的 branchPageElement
func (p *page) branchPageElement(index uint16) *branchPageElement {
// 通过偏移地址的方式获取
return (*branchPageElement)(unsafeIndex(unsafe.Pointer(p), unsafe.Sizeof(*p),
unsafe.Sizeof(branchPageElement{}), int(index)))
}获取到 branchPageElement 后,可以通过 key 方法读取键值,以及通过成员属性直接获取对应子节点的 pgid:
// 获取到 header 后,读取 branch page 对应的 key 值
func (n *branchPageElement) key() []byte {
// 结合 pos 和 ksize,通过偏移地址获得
return unsafeByteSlice(unsafe.Pointer(n), 0, int(n.pos), int(n.pos)+int(n.ksize))
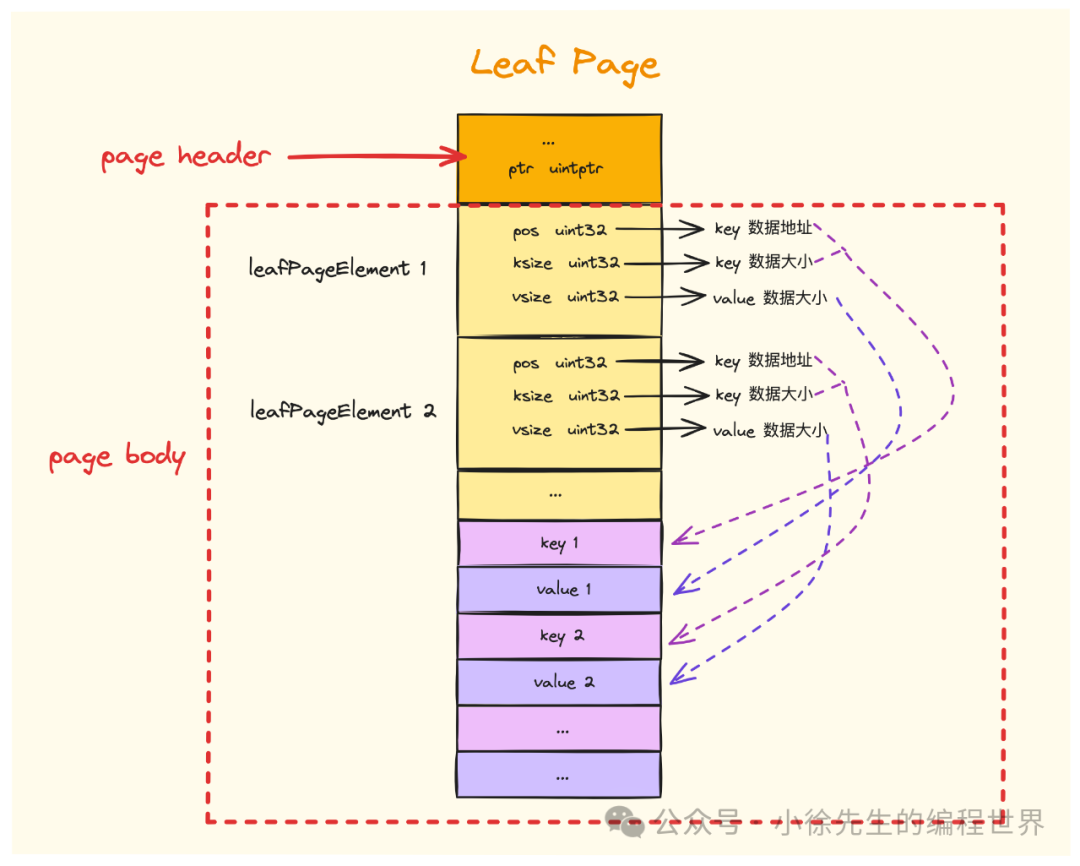
}针对 element page 的结构示意图如上,其中通过 leafPageElement 标识每个内部元素的信息,其中通过 pos 和 ksize 指向 key 值,通过 pos+ksize 结合 vsize 指向 value, 对应的就是叶子节点中的一组 kv 数据:
type leafPageElement struct {
flags uint32 // 标识 kv 对是不是 bucket 类型
pos uint32 // key 起始地址
ksize uint32 // key 的大小,单位 byte
vsize uint32 // value 的大小,单位 byte. value 起始地址为 pos+ksize
}从 branch page 的 header 出发,通过 index 可以获取到指定的 leafPageElement:
// 获取 leaf page 中指定 index 的 leafPageElement
func (p *page) leafPageElement(index uint16) *leafPageElement {
return (*leafPageElement)(unsafeIndex(unsafe.Pointer(p), unsafe.Sizeof(*p),
leafPageElementSize, int(index)))
}获取到 leafPageElement 后,通过地址偏移的方式,就能获取到叶子节点中的指定 kv 对了:
// 获取到 header 后,读取 leaf page 对应的 key 值
func (n *leafPageElement) key() []byte {
// 通过偏移地址读取
i := int(n.pos)
j := i + int(n.ksize)
return unsafeByteSlice(unsafe.Pointer(n), 0, i, j)
}// 获取到 header 后,读取 leaf page 对应的 value 值
func (n *leafPageElement) value() []byte {
// 通过偏移地址读取. value 起始地址为 pos+ksize,因为 value 和 key 是紧挨着的
i := int(n.pos) + int(n.ksize)
j := i + int(n.vsize)
return unsafeByteSlice(unsafe.Pointer(n), 0, i, j)
}综上所述,磁盘中的 b+ 树通过一系列 page 作为节点,枝干节点通过一系列 branchPageElement 建立多叉索引的拓扑结构,通过每个 branchPageElement 中的 pgid 找到指向子节点的引用;叶子节点中则通过一系列 leafPageElement 找到多组 kv 数据的地址
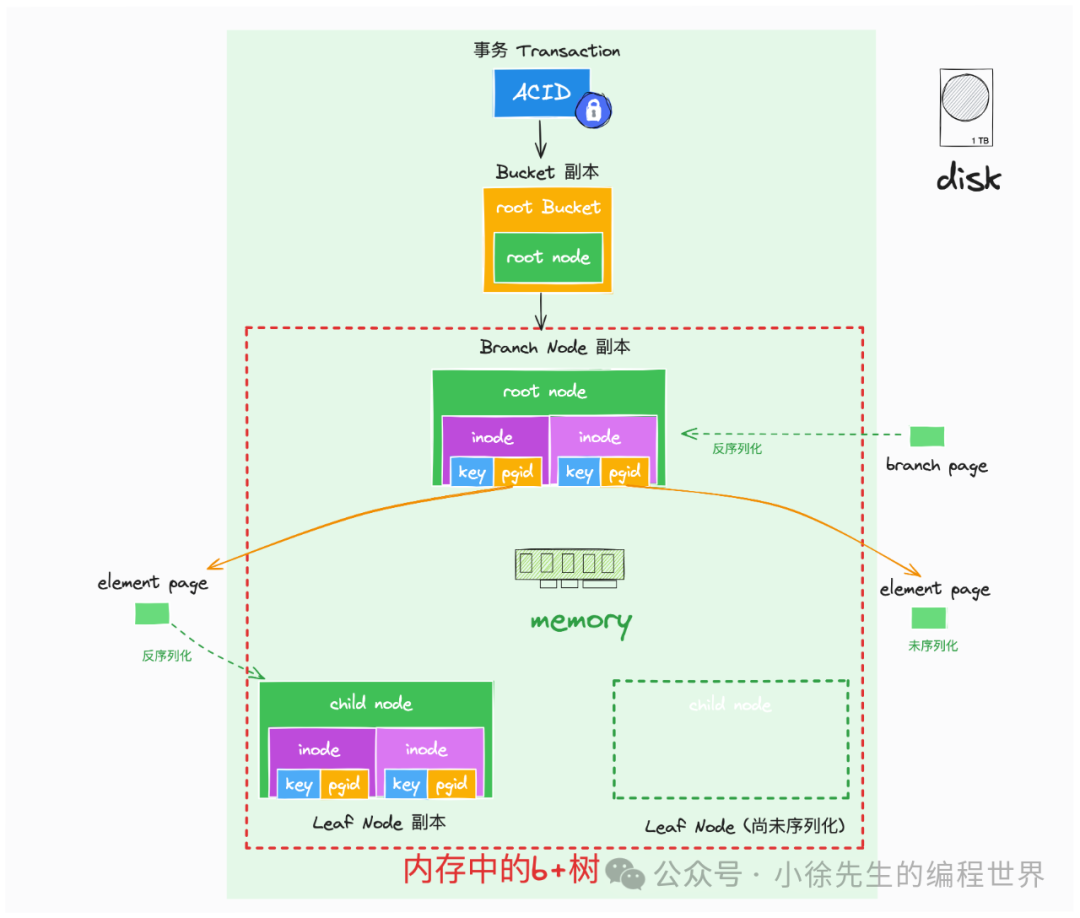
2.3 “内存中的树”
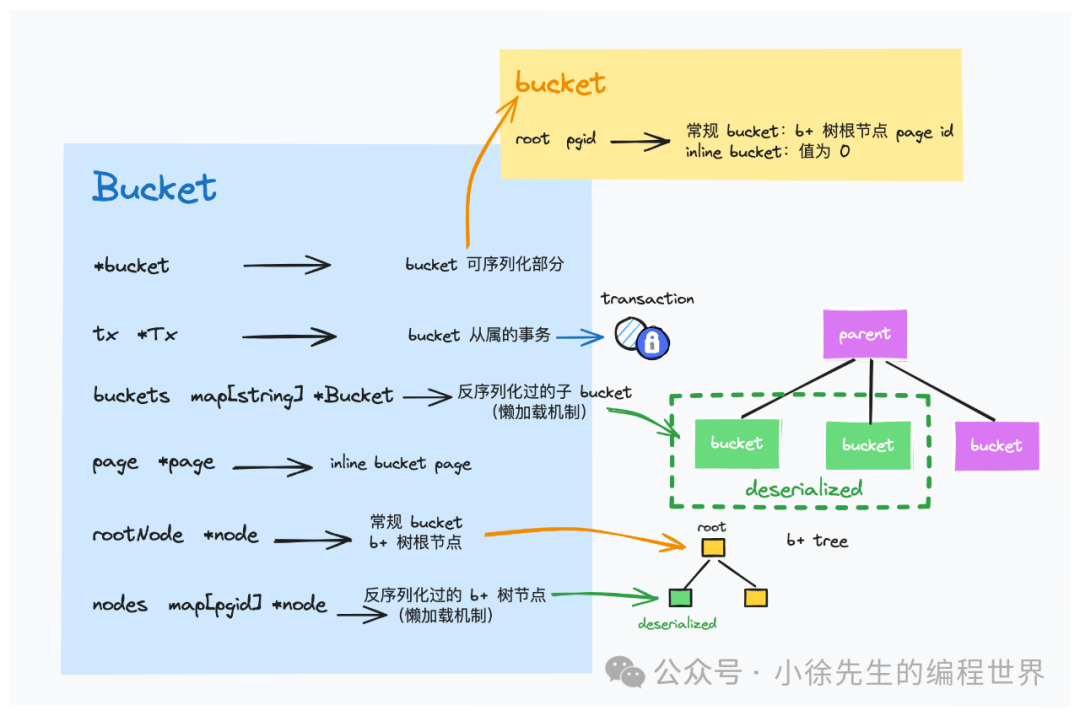
上图展示了内存中的 b+ 树的实现细节,内存中的 b+ 树属于运行时拷贝建立的一个中间态副本,需要从事务实例中开始追溯:
每个事务会基于 copy on write 机制,在内存中拷贝生成一份 root Bucket 副本:
// 事务
type Tx struct {
// ...
// 根 bucket. 是基于 copy on write 在内存中拷贝生成的一份副本
root Bucket
// ...
}每个 Bucket 副本实例中,会持有内存中 b+ 树根节点副本的引用:
// 事务运行时,基于 copy on write 在内存中拷贝生成的一份副本
type Bucket struct {
// ...
rootNode *node // 内存中的 b+ 树根节点
nodes map[pgid]*node // 读写事务过程中,反序列化过的 node 缓存于此
// ...
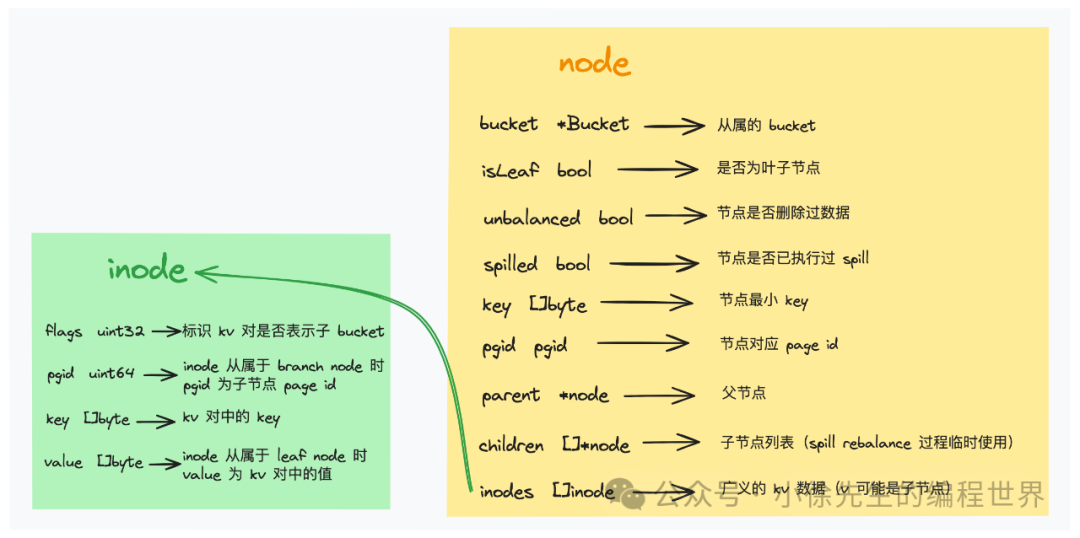
}每个 node 都是基于 branch page 或者 leaf page 反序列化到内存中的一个 b+ 树节点副本,反序列化流程是完全基于懒加载机制推动的,只要在涉及到对该节点内容进行修改时,才会执行该操作:
// 内存中反序列化的一个 b+ 树节点副本
type node struct {
bucket *Bucket // 从属的 bucket
isLeaf bool // 标识其是叶子节点还是枝干节点
unbalanced bool // 标记节点是否有删除过数据,需要在持久化前进行 rebalance 操作
spilled bool // 标记节点是否已经在事务提交过程中执行过 spill 操作
key []byte // 节点中最小的 key
pgid pgid // 节点对应的 page id. 标识其来源,实际上在持久化时会被序列化到一个新的 page 副本中(copy-on-write)
parent *node // 父节点
children nodes // 反序列化过的子节点列表
inodes inodes // 节点内部数据列表. 叶子节点为 key-value 对,枝干节点为 key-child 对
}如果 node 为枝干节点的副本,则会通过一系列 inode 记录指向子节点的引用(指向的是 page,需要修改的时候才会反序列化成 node);
如果 node 为叶子节点的副本,则会通过一系列 inode 记录其中存储的 kv 数据
// b+ 树节点内部的一笔数据. 叶子节点为 key-value 对,枝干节点为 key-child 对
type inode struct {
flags uint32 // 标识 value 是否为 bucket
key []byte // 标识键 key
pgid pgid // 如果 inode 从属于枝干节点,则通过 pgid 指向 child page
value []byte // 如果 inode 从属于叶子节点,则直接通过 value 取值
}2.4 bucket
boltdb 中的 bucket 类似于表的概念,每个 bucket 都会对应一棵独立的 b+ 树.
Bucket 类对应表示一个内存中的 bucket 副本,其核心字段含义展示如上图,其中还包含一个 FillPercent 字段,表示 Bucket 下每个 node 副本在 spill 过程数据填充率需要达到的阈值,默认值为 0.5.
// bucket boltdb 中隔离的一个数据组,可简单理解为表.
// Bucket 是在有事务启动时,基于 copy-on-write 机制生成的一份 bucket 副本
type Bucket struct {
*bucket // bucket header. 需要持久化的数据
tx *Tx // Bucket 从属的事务.
// ...
rootNode *node // Bucket 下的 b+ 树根节点
nodes map[pgid]*node // 事务操作 Bucket 过程中,反序列化过的 node
// bucket 下的 node 填充率阈值. spill 操作时,需要保证拆分出的新节点填充率高于该值
FillPercent float64
}
// 默认 bucket 填充率
const DefaultFillPercent = 0.52.5 cursor
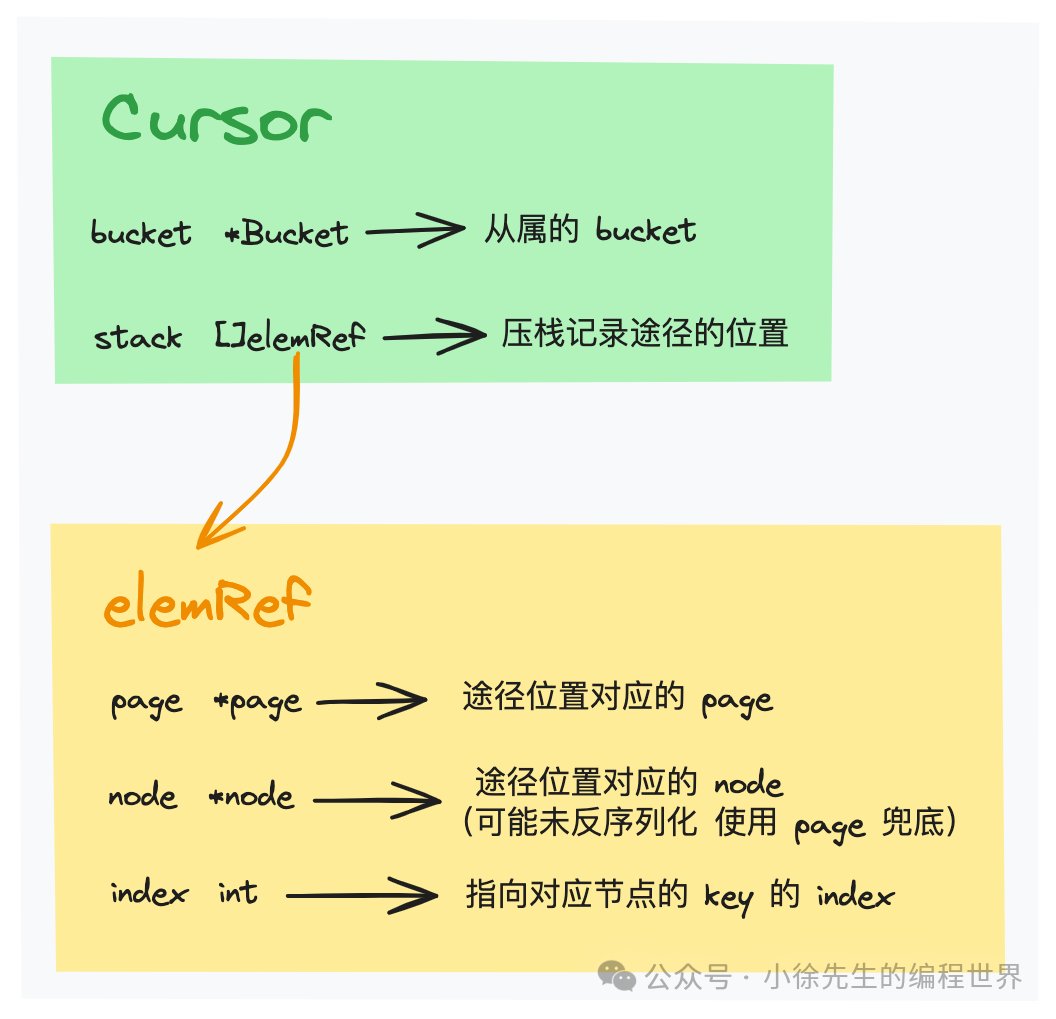
游标 cursor 是 boltdb 用于辅助完成范围操作的检索工具,它会通过一个栈结构 stack 记录某次流程在 b+ 树上的移动路径.
// 与 b+ 树交互时使用的游标工具,通过栈结构记录了检索过程中的移动路径
type Cursor struct {
bucket *Bucket
stack []elemRef // 记录移动路径的栈
}移动路径中的每个 step 对应为一个 elemRef 实例, 其中通过 page 或 node 指向某个 b+ 树节点,通过 index 指向节点中的某个 key.
// cursor 移动过程中的一个 step
type elemRef struct {
page *page // step 位于哪个 page(node 未序列化时使用)
node *node // step 位于哪个 node
index int // step 踩在节点中的哪个 key-value(child)
}// 生成一个新的 bucket 下的游标实例
func (b *Bucket) Cursor() *Cursor {
// ...
// 构造并返回游标实例
return &Cursor{
bucket: b,
stack: make([]elemRef, 0),
}
}3 增删改查
从本章开始,我们一起梳理一下,boltdb 中涉及到 b+ 树数据结构的 crud 流程.
3.1 seek
b+ 树的 crud 很大程度上都是借助游标 cursor 加以实现的,我们首先要理清 cursor 的作用机制,这需要从一个非常核心的方法——cursor.seek 开始谈起:
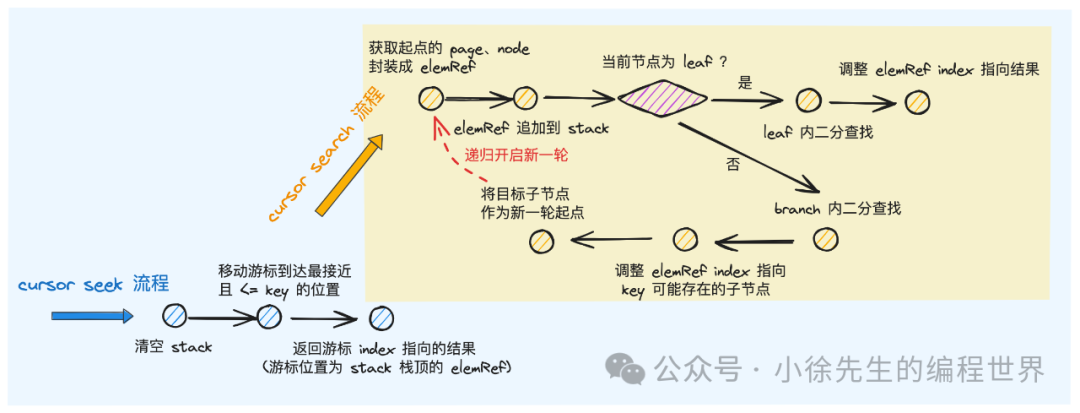
seek 主干流程分为三个步骤:
- 清空游标中的栈结构
- 通过 search 方法,移动游标来到 b+ 树中最接近 key 且 <= key 的位置
- 通过 keyValue 方法返回此时游标所指向的数据
func (c *Cursor) seek(seek []byte) (key []byte, value []byte, flags uint32) {
// 清空栈结构,从头开始检索
c.stack = c.stack[:0]
// 移动游标沿路检索,直到找到目标 key 应该存在的位置
c.search(seek, c.bucket.root)
// 返回 cursor 当前指向位置对应的 key value 值
return c.keyValue()
}search 方法的作用是,沿着 pgId 对应节点作为起点出发,将 cursor 移动到 <= key 且最接近 key 的位置:
- 获取 pgId 对应的节点,倘若已完成反序列化,则使用 node,否则使用 page
- 将当前节点封装成一个 elemRef,压入 cursor 的 stack 中
- 倘若当前节点是叶子节点,则通过 nsearch 方法在叶子节点中检索数据
- 倘若当前节点是枝干节点,则根据节点是否已反序列化成 node,通过 searchNode 或者 searchPage 方法,在子节点中完成后续的检索流程
func (c *Cursor) search(key []byte, pgId pgid) {
// 根据 pgid 在 bucket 中获取节点. 如果反序列化过 node 就用 node,否则就用 page
p, n := c.bucket.pageNode(pgId)
// 包装成移动路径中的一个 step
e := elemRef{page: p, node: n}
// 追加到记录移动路径对应的栈结构中
c.stack = append(c.stack, e)
// 如果已经来到叶子节点,则在节点内部检索结果
if e.isLeaf() {
c.nsearch(key)
return
}
// 否则继续在枝干节点上检索
if n != nil {
c.searchNode(key, n)
return
}
c.searchPage(key, p)
}倘若来到叶子节点,通过 nsearch 方法在其中检索数据:
- 获取栈顶的叶子节点
- 通过二分查找的方法,找到叶节点中首个 >= key 的 kv 对
- 倘若找到的结果恰好等于 key 值,则当前 step 的 index 指向该位置,否则 index 倒退一步,指向 < key 但是最接近 key 的位置
通过这个 nsearch 流程也能进一步看出内存中 b+ 树副本的懒加载机制,在读流程检索 b+ 树的过程中,哪怕某个节点没有反序列化过也没有关系,可以通过获取对应 page 完成数据的检索操作.
// 在当前栈顶 step 所在的叶子节点中检索,使得 index 指向首个 >= key 的位置
func (c *Cursor) nsearch(key []byte) {
// 获取栈顶 step(当前所在位置)
e := &c.stack[len(c.stack)-1]
p, n := e.page, e.node
// 如果有反序列化好的 node,则使用 node
if n != nil {
// 二分查找,找到首个 >= key 的 inode 对应的 index
index := sort.Search(len(n.inodes), func(i int) bool {
return bytes.Compare(n.inodes[i].key, key) != -1
})
e.index = index
return
}
// node 未反序列化,则通过 page 来检索
// 获取 leaf page 下的全量 leafPageElement
inodes := p.leafPageElements()
// 二分查找,找到首个 >= key 的 leafPageElement 对应的 index
index := sort.Search(int(p.count), func(i int) bool {
return bytes.Compare(inodes[i].key(), key) != -1
})
e.index = index
}倘若当前还处在枝干节点,则根据当前节点是否以反序列化成 node,选择调用 searchNode 或者 searchPage 方法来完成后续检索流程:
- 针对当前节点内的元素二分查找,找到首个 >= key 的元素
- 倘若找到的结果恰好等于 key 值,则当前 step 的 index 指向该元素,否则 index 倒退一步,指向 < key 但是最接近 key 的元素
- 以找到的目标元素作为新的起点,递归调用 search 方法,开启新的轮次
// 当前枝干节点已反序列化成 node
func (c *Cursor) searchNode(key []byte, n *node) {
// 是否与某个 inode 的 key 相等
var exact bool
// 二分检索,找到首个 >= key 的 inode
index := sort.Search(len(n.inodes), func(i int) bool {
// 对比 inode 的 key 和目标 key
ret := bytes.Compare(n.inodes[i].key, key)
if ret == 0 { // 如果相同,标识 exact 为 true
exact = true
}
// 找到首个 >= 目标 key 的 inode
return ret != -1
})
// 如果 inode 首个 key 不相同而是更大,则 index 往前倒退一位
if !exact && index > 0 {
index--
}
// 记录当前 step 指向的 index 位置
c.stack[len(c.stack)-1].index = index
// 递归调用 search 方法,以子节点为起点开始下一轮检索
c.search(key, n.inodes[index].pgid)
}// 当前枝干节点未反序列化成 node
func (c *Cursor) searchPage(key []byte, p *page) {
// 获取 branch page 内的所有 branchPageElement,通过地址偏移的方式
inodes := p.branchPageElements()
// 是否与某个 inode 的 key 相等
var exact bool
// 二分检索,找到首个 >= key 的 inode
index := sort.Search(int(p.count), func(i int) bool {
// 对比 inode 的 key 和目标 key
ret := bytes.Compare(inodes[i].key(), key)
// 和 inode 的 key 相同,exact 置为 true
if ret == 0 {
exact = true
}
// 返回首个 >= key 的 inode
return ret != -1
})
// 如果 inode 首个 key 不相同而是更大,则 index 往前倒退一位
if !exact && index > 0 {
index--
}
// 记录当前 step 指向的 index 位置
c.stack[len(c.stack)-1].index = index
// 递归调用 search 方法,以子节点为起点开始下一轮检索
c.search(key, inodes[index].pgid)
}当 cursor 移动到目标位置后,可以通过 keyValue 方法取出对应的 kv 结果:
- 取出栈顶 step
- 倘若 step 对应节点没有数据,或者 index 非法,则返回 nil
- 倘若节点已反序列化成 node,则取出 index 对应的 inode,返回 kv 数据
- 倘若节点未反序列化成 node,则通过 page 取出 index 对应的 leafPageElement,再通过地址偏移的方式,返回 kv 数据
func (c *Cursor) keyValue() ([]byte, []byte, uint32) {
// 获取栈顶的 step
ref := &c.stack[len(c.stack)-1]
// 如果 step 所在的节点没有数据,或者指向的 index 越界,则返回 nil
if ref.count() == 0 || ref.index >= ref.count() {
return nil, nil, 0
}
// 倘若节点反序列已经反序列化成 node,则根据 index 获取到 inode,并返回 key value
if ref.node != nil {
inode := &ref.node.inodes[ref.index]
return inode.key, inode.value, inode.flags
}
// 未反序列化成 node,则根据 index 获取到对应的 leafPageElement
elem := ref.page.leafPageElement(uint16(ref.index))
// 通过地址偏移的方式,获取到 key value
return elem.key(), elem.value(), elem.flags
}3.2 node
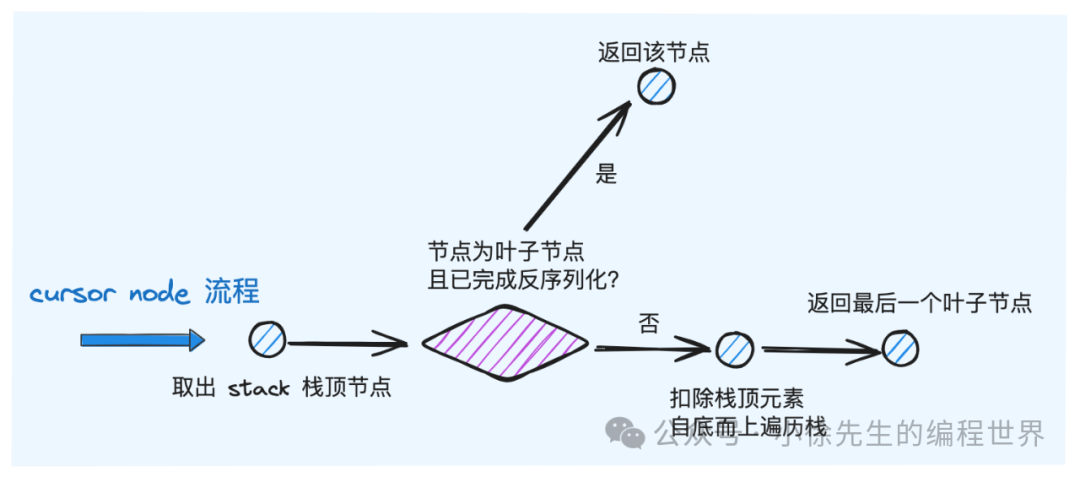
cursor.node 方法,用于返回游标移动路径中,最后一个叶子节点 node 副本:
- 倘若栈顶 step 对应节点已反序列成 node,并且是叶子节点,则直接返回该 node 副本
- 排除栈顶 step 后,自栈底向上遍历,找到最后一个叶子节点,确保将其反序列化成 node 副本后返回
func (c *Cursor) node() *node {
// ...
// 1 返回栈顶对应的 node. 如果 node 已经反序列化了并且是叶子节点,直接返回即可
if ref := &c.stack[len(c.stack)-1]; ref.node != nil && ref.isLeaf() {
return ref.node
}
// 使用 b+ 树根节点进行兜底(倘若一个节点都)
var n = c.stack[0].node
if n == nil {
n = c.bucket.node(c.stack[0].page.id, nil)
}
// 扣除栈顶元素后,后开始正序遍历(从根节点出发)
for _, ref := range c.stack[:len(c.stack)-1] {
// 按照移动路径中每个 step 的 index 指引前进的方向(找到要通往的子节点在父节点 inodes 中的 index)
n = n.childAt(ref.index)
}
// ...
// 返回检索到的 node
return n
}返回 node 中对应 index 的子节点:
func (n *node) childAt(index int) *node {
// ...
return n.bucket.node(n.inodes[index].pgid, n)
}// 从 bucket 中的返回 page 对应的 node 副本. 如果没反序列化过,会进行反序列化
func (b *Bucket) node(pgId pgid, parent *node) *node {
// 如果对应 node 已经在 Bucket 反序列化过,则直接复用
if n := b.nodes[pgId]; n != nil {
return n
}
// 构造 node 副本实例
n := &node{bucket: b, parent: parent}
if parent == nil {
b.rootNode = n
} else {
parent.children = append(parent.children, n)
}
// 兼容 inline bucket 类型
var p = b.page
if p == nil { // 非 inline bucket,则根据 pg id 取出对应的 page
p = b.tx.page(pgId) // 底层基于 pgid + pageSize,在 mmap 中通过地址偏移的方式获取到
}
// 读取 page 内容,反序列化到 node 实例中
n.read(p)
// 缓存 node
b.nodes[pgId] = n
// ...
return n
}3.3 put
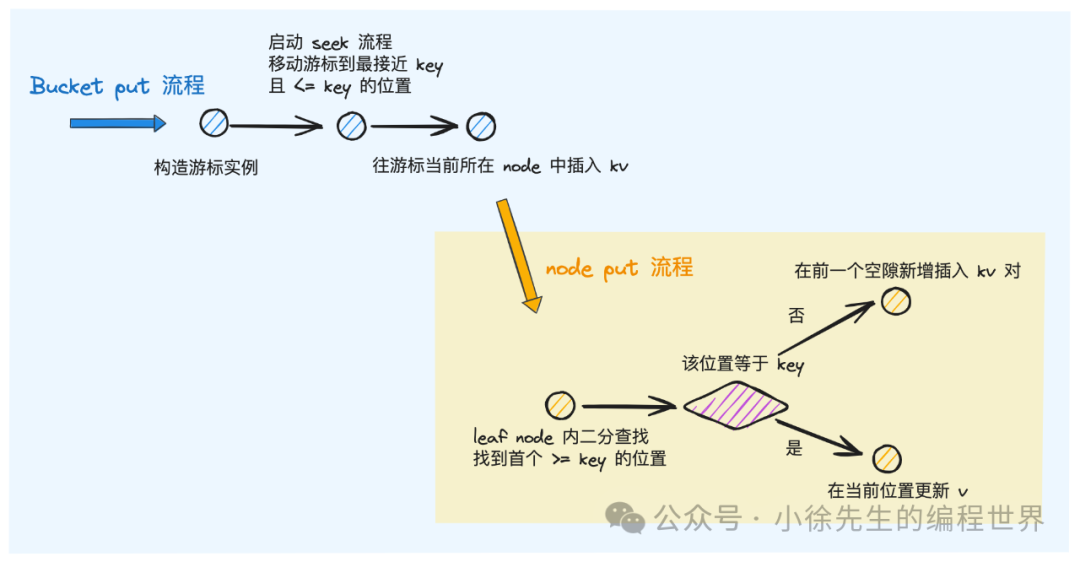
通过 Bucket.Put 方法,能够实现往指定表中插入或者更新一组 kv 数据的操作:
- 构造游标 cursor 实例
- 移动 cursor,到达最接近 key 且 <= key 的位置
- 借助 node.put 方法,在节点中完成 kv 数据的写入:
- 如果节点中存在 key 相等的 inode,则对 inode 的 value 进行更新
- 否则为 kv 对构造新的 inode 实例,根据 key 的升序,找到合适的空隙完成插入
// 往 Bucket 下的 b+ 树中写入一笔 kv 对数据.
func (b *Bucket) Put(key []byte, value []byte) error {
// ...
// 1 构造一个新的游标实例
c := b.Cursor()
// 2 借助游标,移动到 key 应该被写入的位置,并且通过栈结构记录过程中的移动路径
k, _, flags := c.seek(key)
// ...
// 3 在对应位置中写入 key-value 对
key = cloneBytes(key)
c.node().put(key, key, value, 0, 0)
return nil
}// 往 node 中插入一组 key-value 对
func (n *node) put(oldKey, newKey, value []byte, pgId pgid, flags uint32) {
// ...
// 找到 node 中首个 >= oldKey 的 inode 对应的 index
index := sort.Search(len(n.inodes), func(i int) bool { return bytes.Compare(n.inodes[i].key, oldKey) != -1 })
// exact 标识:index 对应 innode 的 key 是否等于 oldKey
exact := (len(n.inodes) > 0 && index < len(n.inodes) && bytes.Equal(n.inodes[index].key, oldKey))
if !exact { // 倘若不等,则需要在其之前插入一个新的 inode,写入 newKey
n.inodes = append(n.inodes, inode{})
copy(n.inodes[index+1:], n.inodes[index:])
}
// 找到 index 指向的 innode
inode := &n.inodes[index]
// 写入对应的 newKey、value、flags、pgID 等信息
inode.flags = flags
inode.key = newKey
inode.value = value
inode.pgid = pgId
// ...
}3.4 get
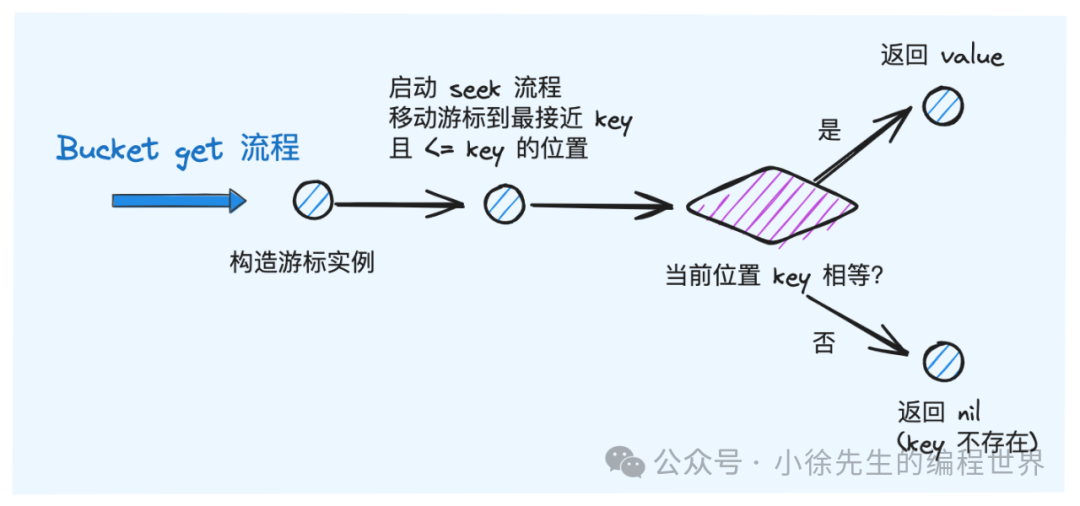
通过 Bucket.Gut 方法,能够从表中获取 key 对应的 value:
- 构造游标 cursor 实例
- 移动 cursor,到达最接近 key 且 <= key 的位置
- 取出 cursor 指向的元素,校验元素的 key 是否与检索的 key 相等,如果相等,说明 key 存在,返回 value;否则说明 key 不存在,返回 nil
// 从 Bucket 中获取 key 对应的 value
func (b *Bucket) Get(key []byte) []byte {
// 构造游标,并根据 key 移动到指定位置
k, v, flags := b.Cursor().seek(key)
// 倘若游标所在位置不是叶子节点,说明没有满足要求的 kv 对,返回空
if (flags & bucketLeafFlag) != 0 {
return nil
}
// 游标所在位置 key 不等,说明没有满足要求的 kv 对,返回空
if !bytes.Equal(key, k) {
return nil
}
// 返回 value
return v
}3.5 delete
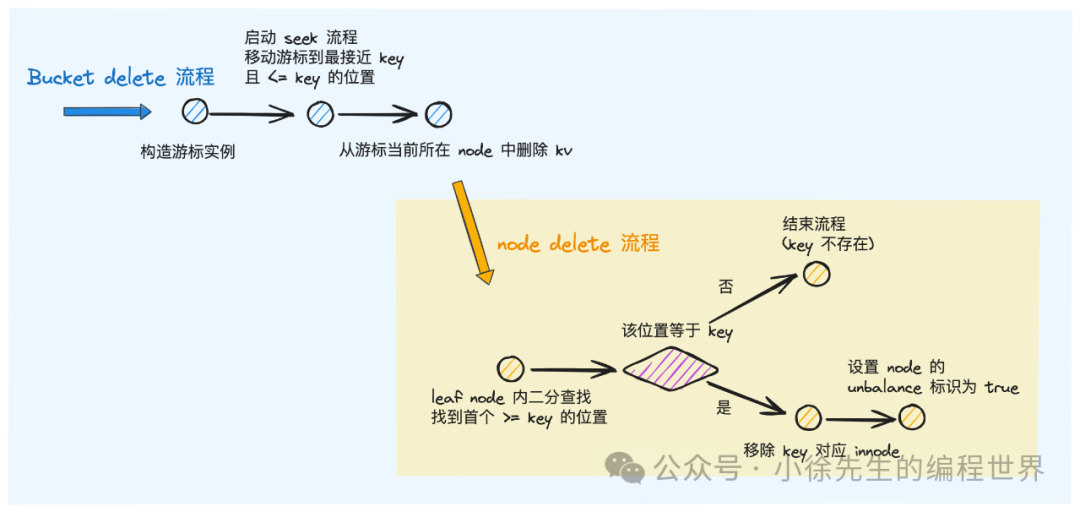
通过 Bucket.Delete 方法,能够实现在表中删除 key 的操作:
- 构造游标 cursor 实例
- 移动 cursor,到达最接近 key 且 <= key 的位置
- 取出 cursor 所指向的元素,倘若元素的 key 与拟删除 key 不等,则说明 key 不存在,结束流程
- 借助 node.del 方法,从 node 中移除 key 对应的 inode
// 从 bucket 中删除某个 key
func (b *Bucket) Delete(key []byte) error {
// ...
// 构造 bucket 下的游标实例
c := b.Cursor()
// 移动游标,根据 key 移动到指定位置
k, _, flags := c.seek(key)
// 如果当前所在位置 key 不等,说明 kv 对不存在,返回 nil
if !bytes.Equal(key, k) {
return nil
}
// ...
// 从游标当前所在节点中删除对应的 key
c.node().del(key)
return nil
}// 从 node 副本中删除某个 key
func (n *node) del(key []byte) {
// 在 node 中二分查找,找到首个 >= key 的 inode
index := sort.Search(len(n.inodes), func(i int) bool { return bytes.Compare(n.inodes[i].key, key) != -1 })
// 如果 innode 的 key 不等,说明 key 不存在,直接返回
if index >= len(n.inodes) || !bytes.Equal(n.inodes[index].key, key) {
return
}
// 从 inodes 中删除 key 对应的 innode
n.inodes = append(n.inodes[:index], n.inodes[index+1:]...)
// 设置 node 为 unbalanced 状态,在持久化前需要执行 rebalance 操作
n.unbalanced = true
}4 平衡调整
针对 b+ 树而言,最复杂的流程莫过于——因为写入或者删除操作导致其平衡性遭到破坏,进一步需要补偿执行的 rebalance 和 spill 操作.
在前文中我也提到了,由于内存中的 b+ 树本质上是一个读写事务在执行过程中建立的一份临时副本,因此为了保证操作性能,在事务运行过程中可以允许这份副本暂时被打破平衡性,但会保证在其因事务提交而被落盘为磁盘上持久化的 b+ 树之时完成平衡性的调整.
4.1 rebalance
在事务提交时,首先会针对内存中的 b+ 树副本执行 rebalance 流程:
func (tx *Tx) Commit() error {
// ...
// rebalance ...
tx.root.rebalance()
// ...
opgid := tx.meta.pgid
// spill ...
if err := tx.root.spill(); err != nil {
tx.rollback()
return err
}
// 脏数据页落盘...
// meta page 落盘...
return nil
}rebalance 流程以 Bucket 副本为单元分组执行:
- 针对 Bucket 下所有反序列化过的 node 副本执行 rebalance(只有 node 被反序列过,才代表其中可能有数据调整)
- 针对 Bucket 下所有反序列过的子 Bucket 副本执行 rebalance(只有 bucket 被反序列过,才代表其中可能有数据调整)
func (b *Bucket) rebalance() {
// 针对 bucket 下的所有 node 副本进行 rebalance
// 只有被反序列化成 node 副本的节点才可能有过修改
for _, n := range b.nodes {
n.rebalance()
}
// 针对所有反序列化过的子 bucket 副本进行 rebalance
// 只有被反序列化成 bucket 副本的桶才可能有过修改
for _, child := range b.buckets {
child.rebalance()
}
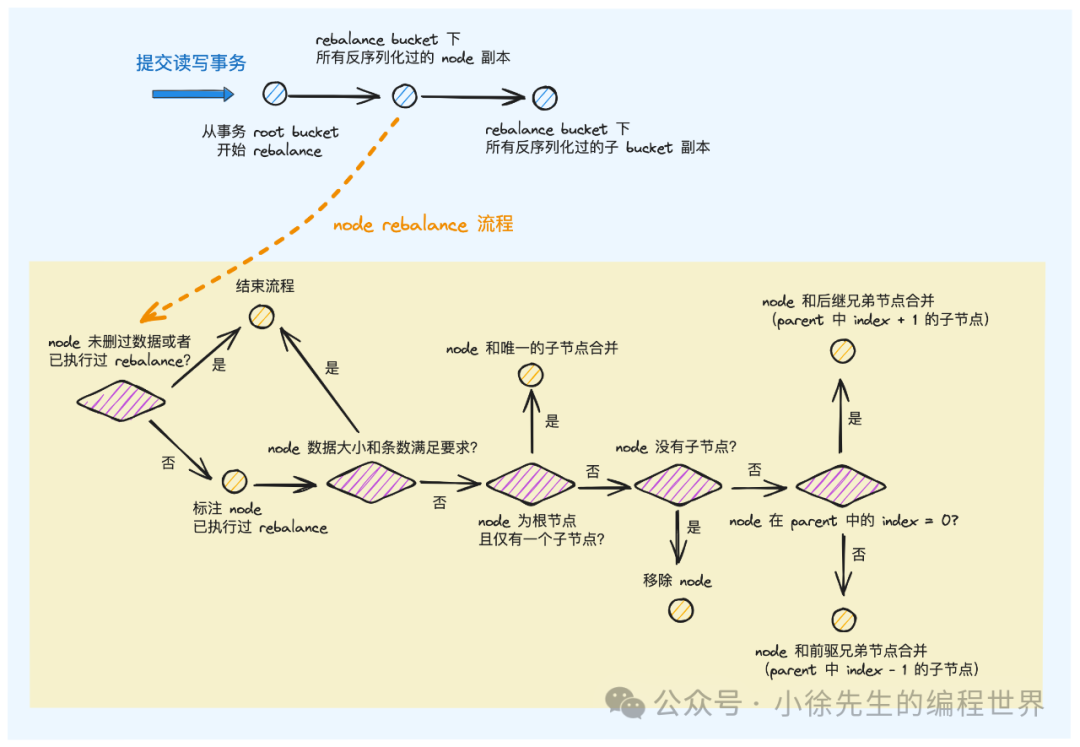
}下面拆解核心方法——node.rebalance:
- 倘若 node 副本没有删除过数据,或者已经执行过 rebalance,则提前结束流程
- 设置当前 node 副本 unbalanced 标识为 false,代表已经执行过 rebalance
- 校验 node 副本的数据大小以及元素数量,如果数据大小 > pageSize/4 且元素数 > minKeys,则无需 rebalance,结束流程
- 如果当前 node 副本是 root 节点,则只有一个子节点,则与子节点合并成一个节点,结束流程
- 如果当前 node 副本因为数据删除操作导致其中数据已经为空,则直接移除该节点,结束流程
- 将当前 node 副本在父节点中的 index 为 0,则与后继兄弟节点合并成一个节点;否则与前驱兄弟节点合并成一个节点
func (n *node) rebalance() {
// 节点没有删除过数据,则无需 rebalance
if !n.unbalanced {
return
}
// 当前已经在执行 rebalance 流程,为避免重复执行,将 unbalanced 置为 false
n.unbalanced = false
// ...
// 如果节点填充数据量 > pageSzie/4 并且 key 满足最小数量要求 (叶子节点多于 1 个 key,枝干节点多于 2 个 key),则不需要进行 rebalance
var threshold = n.bucket.tx.db.pageSize / 4
if n.size() > threshold && len(n.inodes) > n.minKeys() {
return
}
// 如果当前 node 是 root,则有特殊处理
if n.parent == nil {
// 如果 root 为枝干节点,并且只有一个 inode,需要和 inode 合并
if !n.isLeaf && len(n.inodes) == 1 {
// 获取唯一的 child node
child := n.bucket.node(n.inodes[0].pgid, n)
// copy child node 的信息
n.isLeaf = child.isLeaf
n.inodes = child.inodes[:]
n.children = child.children
// 将 child node 的所有孩子的 parent 置为自己
for _, inode := range n.inodes {
if child, ok := n.bucket.nodes[inode.pgid]; ok {
child.parent = n
}
}
// 移除 child node
child.parent = nil
delete(n.bucket.nodes, child.pgid)
child.free()
}
return
}
// 如果当前节点没有 inode,则直接移除当前节点
if n.numChildren() == 0 {
n.parent.del(n.key)
n.parent.removeChild(n)
delete(n.bucket.nodes, n.pgid)
n.free()
// 递归 rebalance 父节点
n.parent.rebalance()
return
}
// 断言:父节点必然至少有两个孩子节点. 因为父节点是枝干节点,孩子节点数至少为 2,这是 boltdb 实现 b+ 树的规范
_assert(n.parent.numChildren() > 1, "parent must have at least 2 children")
// 走常规流程,进行 rebalance 操作
// 如果当前 node 在 parent 中的 index = 0,则和后继兄弟节点合并
// 如果当前 node 在 parent 中的 index > 0,则和前驱兄弟节点合并
var target *node
var useNextSibling = (n.parent.childIndex(n) == 0)
if useNextSibling {
target = n.nextSibling()
} else {
target = n.prevSibling()
}
// 和后继节点合并
if useNextSibling {
// 遍历后继节点的所有 child node,将其 parent 指向自己,并添加到自己的 children 列表中
for _, inode := range target.inodes {
if child, ok := n.bucket.nodes[inode.pgid]; ok {
child.parent.removeChild(child)
child.parent = n
child.parent.children = append(child.parent.children, child)
}
}
// 当前节点 inodes 列表追加后继节点的所有 inode
n.inodes = append(n.inodes, target.inodes...)
// 从 parent 中删除后继节点,包含删除 b+ 树中的 kv 数据以及从 parent node 中的 children list 中移除
n.parent.del(target.key)
n.parent.removeChild(target)
// 从 bucket 的 nodes 缓存中移除后继节点
delete(n.bucket.nodes, target.pgid)
target.free()
} else { // 和前驱节点合并
// 遍历自己的所有 child node,将其 parent 指向前驱节点,并添加到前驱节点的 children 列表中
for _, inode := range n.inodes {
if child, ok := n.bucket.nodes[inode.pgid]; ok {
child.parent.removeChild(child)
child.parent = target
child.parent.children = append(child.parent.children, child)
}
}
// 前驱节点的 inodes 中追加当前节点的所有 inode
target.inodes = append(target.inodes, n.inodes...)
// 从 parent 中删除当前节点,包含删除 b+ 树中的 kv 数据以及从 parent node 中的 children list 中移除
n.parent.del(n.key)
n.parent.removeChild(n)
// 从 bucket 的 nodes 缓存中移除当前节点
delete(n.bucket.nodes, n.pgid)
n.free()
}
// 递归 rebalance parent
n.parent.rebalance()
}下面附上上述流程涉及到的几个支线方法:
- minKeys:获取一个 node 副本中最少应该存在的 key 数量——针对叶子节点,key 数应该 > 1,针对枝干节点,key 数应该 > 2
func (n *node) minKeys() int {
if n.isLeaf {
return 1
}
return 2
}prevSibling——获取 node 副本的前驱兄弟节点:
- 获取 node 在 parent 中的 index
- 取出 parent 中 index - 1 对应的子 node 副本
func (n *node) prevSibling() *node {
if n.parent == nil {
return nil
}
index := n.parent.childIndex(n)
if index == 0 {
return nil
}
return n.parent.childAt(index - 1)
}nextSibling——获取 node 副本的后继兄弟节点:
- 获取 node 在 parent 中的 index
- 取出 parent 中 index + 1 对应的子 node 副本
func (n *node) nextSibling() *node {
if n.parent == nil {
return nil
}
index := n.parent.childIndex(n)
if index >= n.parent.numChildren()-1 {
return nil
}
return n.parent.childAt(index + 1)
}4.2 spill
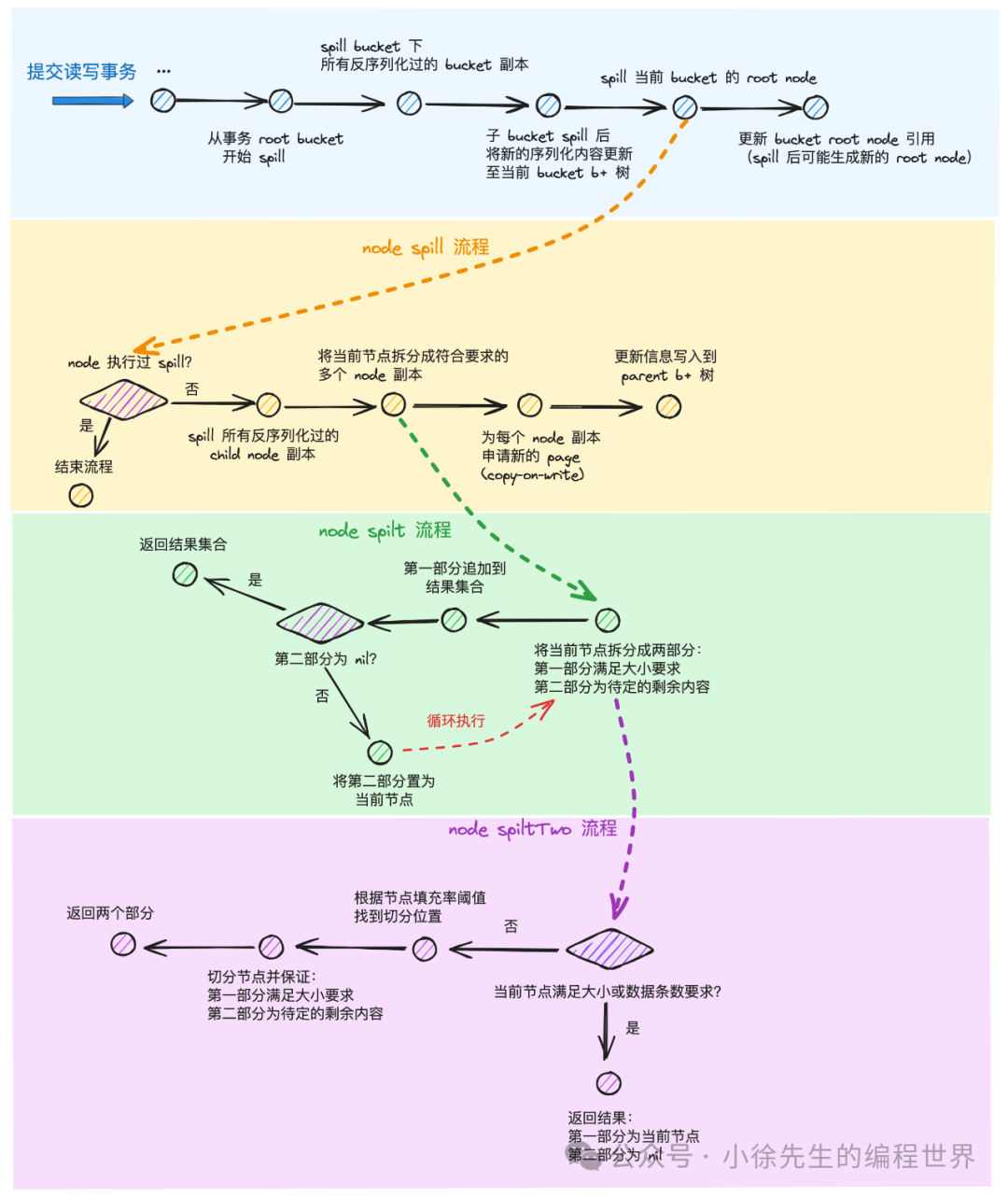
事务提交流程中,完成 rebalance 操作后,就会进一步执行 spill 操作. 且 spill 流程不仅完成大节点的拆分,还会基于 copy-on-write 机制为所有反序列化过的 node 分配新的 page 副本:
func (tx *Tx) Commit() error {
// ...
// rebalance ...
tx.root.rebalance()
// ...
opgid := tx.meta.pgid
// spill ...
if err := tx.root.spill(); err != nil {
tx.rollback()
return err
}
// 脏数据页落盘...
// meta page 落盘...
return nil
}spill 流程以 Bucket 副本为单元分组执行:
- 针对 Bucket 副本下所有反序列化过的子 bucket 副本执行 spill,并生成新的序列化内容,组装成 kv 对的形式写入到当前 Bucket 副本的 b+ 树中
- 沿着当前 Bucket 下 b+ 树根节点开始依次以 node 副本的维度执行 spill 操作
// spill 拆分 bucket
func (b *Bucket) spill() error {
// 针对所有反序列化过的子 bucket,尝试进行 spill
for name, child := range b.buckets {
var value []byte
// 针对 inline bucket,无需 spill. 直接序列化
if child.inlineable() {
child.free()
value = child.write()
} else {
// 针对常规的子 bucket,需要递归执行 spill 操作
if err := child.spill(); err != nil {
return err
}
// 深拷贝一份 child bucket header 的副本
value = make([]byte, unsafe.Sizeof(bucket{}))
var bucket = (*bucket)(unsafe.Pointer(&value[0]))
*bucket = *child.bucket
}
// 如果 child 没有数据,直接跳过
if child.rootNode == nil {
continue
}
// 构造一个当前 bucket 的 cursor 实例
var c = b.Cursor()
// 移动 cursor,走到 child bucket 所在 kv 对的位置
k, _, flags := c.seek([]byte(name))
// 更新 kv 对内容,value 更新为 spill 后的 child bucket 的序列化数据
c.node().put([]byte(name), []byte(name), value, 0, bucketLeafFlag)
}
// 如果当前 bucket 没有数据,则无需 spill 直接返回
if b.rootNode == nil {
return nil
}
// 从 root node 开始 spill 拆分
if err := b.rootNode.spill(); err != nil {
return err
}
// spill 后可能会出现新的 root 节点,因此尝试更新引用
b.rootNode = b.rootNode.root()
// ...
// 更新 root 节点对应 page id
b.root = b.rootNode.pgid
return nil
}node.spill 基于 node 副本进行 spill 拆分,并针对拆分后的每个 node 副本依次分配新 page 的核心方法:
- 倘若 node 已经执行过 spill,则提前结束流程
- 优先针对每个反序列化过的 child node 副本,依次执行 spill 流程
- 通过 node.split 方法,将当前节点拆分成多个符合数据填充率要求的 node 副本
- 依次为每个 node 副本申请新的 page 副本,体现 copy-on-write 机制
func (n *node) spill() error {
var tx = n.bucket.tx
// 节点已经 spill 过,直接返回
if n.spilled {
return nil
}
// 对反序列化过的 child node 进行排序
sort.Sort(n.children)
// 针对每个反序列化过的 child node 先进行 spill 操作
for i := 0; i < len(n.children); i++ {
if err := n.children[i].spill(); err != nil {
return err
}
}
// children 置为空. 因为能走到 spill 流程必然是提交事务的时刻,后续 children 已经不需要用到了
n.children = nil
// 将当前 node 拆分成多个符合要求的 node
var nodes = n.split(uintptr(tx.db.pageSize))
// 遍历所有拆分出来的新节点
for _, node := range nodes {
// 如果 node 对应 page id > 0,代表复用了之前的 page,则需要对 page 进行 free.
// 因为当前 node 要被写入到一个新的脏数据 page 副本中了
if node.pgid > 0 {
tx.db.freelist.free(tx.meta.txid, tx.page(node.pgid))
node.pgid = 0
}
// 根据 node 数据量大小结合 pageSize 设定,计算出 node 需要的 page 数量
// 申请分配指定数量的可用 page. 此时优先从 freelist 获取,如果 freelist 资源不足,则重新进行一轮 mmap 作扩容
// 此处如果要分配的 page 数量 > 1,则会通过 overflow 进行拼接. 逻辑意义上仍是一个"page"
p, err := tx.allocate((node.size() + tx.db.pageSize - 1) / tx.db.pageSize)
// node pg id 指向申请到的可用 page 的首个 page 的 id
node.pgid = p.id
// node 内容序列化到 page 中
node.write(p)
// 标识 node 已经 spill 过了
node.spilled = true
// parent 存在,则跟新对应的 inodes 和 b+ 树中的 kv 数据
if node.parent != nil {
var key = node.key
if key == nil {
key = node.inodes[0].key
}
// 写入到 parent b+ 树中
node.parent.put(key, node.inodes[0].key, nil, node.pgid, 0)
// 更新 parent node 的 inodes 内容
node.key = node.inodes[0].key
// ...
}
// ...
}
// 如果 spill 过程中给 node 拆出了一个新的 parent,则需要递归对其 spill
if n.parent != nil && n.parent.pgid == 0 {
n.children = nil
return n.parent.spill()
}
return nil
}下面看看,如何实现将一个节点拆分成多个合规的 node 副本:
- 循环将 node 副本拆分成两个部分,每次保证第一部分大小合规,追加到结果集合中
- 取第二部分做处理,倘若第二部分为空,终止流程;否则以第二部分为起点,开始新一轮循环
func (n *node) split(pageSize uintptr) []*node {
var nodes []*node
node := n
for {
// 首先将当前 node 拆分成两部分:
// - 第一部分:一定满足大小要求
// - 第二部分:如果为 nil,则拆分结束;如果大小仍不合规,则针对第二部分递归拆分
a, b := node.splitTwo(pageSize)
nodes = append(nodes, a)
// 第二部分为 nil,则拆分结束
if b == nil {
break
}
// node 指向第二部分,递归对第二部分执行上述流程
node = b
}
return nodes
}在 node.splitTwo 方法中:
- 首先校验当前节点是否合规,是的话直接返回当前节点作为第一部分,第二部分置为空
- 根据 bucket 设置的数据填充率阈值,通过 splitIndex 方法找到当前 node 副本的切分边界,将 node 切分成两部分返回,保证第一部分大小合规
// 根据传入的 pageSize 阈值,将 node 拆分为两部分,保证第一部分一定满足要求
func (n *node) splitTwo(pageSize uintptr) (*node, *node) {
// 如果当前 node 的 inode 数量 <= 4 或者数据大小小于 pageSize,则直接返回不作拆分
if len(n.inodes) <= (minKeysPerPage*2) || n.sizeLessThan(pageSize) {
return n, nil
}
// 根据 bucket 设置的填充率计算出 spill 阈值 threshold
var fillPercent = n.bucket.FillPercent
if fillPercent < minFillPercent {
fillPercent = minFillPercent
} else if fillPercent > maxFillPercent {
fillPercent = maxFillPercent
}
threshold := int(float64(pageSize) * fillPercent)
// 根据 threshold,得出 split 切分之处的 index. 从 index 开始往右的部分为切分出来的第二部分
splitIndex, _ := n.splitIndex(threshold)
// 如果 node 原本为 root,需要构造出一个新的 root. 因为 node 要被拆分了
if n.parent == nil {
n.parent = &node{bucket: n.bucket, children: []*node{n}}
}
// 拆分后的第二部分内容暂时存放在 next 实例当中
next := &node{bucket: n.bucket, isLeaf: n.isLeaf, parent: n.parent}
// next 追加到 parent 的 children 中
n.parent.children = append(n.parent.children, next)
// 将 node 的 inodes 沿着 splitIndex 一分为二,第二部分分给 next
next.inodes = n.inodes[splitIndex:]
n.inodes = n.inodes[:splitIndex]
// ...
// 返回拆分后得到的两部分
return n, next
}// 根据 thresold,找到 node 的拆分边界
func (n *node) splitIndex(threshold int) (index, sz uintptr) {
sz = pageHeaderSize
// 遍历 node 的 inodes
for i := 0; i < len(n.inodes)-minKeysPerPage; i++ {
index = uintptr(i)
inode := n.inodes[i]
// 计算得到 pageElement + key + value 三部分总大小
elsize := n.pageElementSize() + uintptr(len(inode.key)) + uintptr(len(inode.value))
// 如果加上当前 inode 后,前半部分大小超过阈值,则找到拆分边界, index 就是后半部分的起点
if index >= minKeysPerPage && sz+elsize > uintptr(threshold) {
break
}
// 每遍历完一个 inode,将 elsize 累加到 sz
sz += elsize
}
return
}至此,b+树篇正文结束.
5 展望
本文是 etcd 存储引擎系列的第三篇,带着大家一起深入了解了 b+树理论模型以及 boltdb 针对该模块的实现细节. 在此回顾整个系列的研究进程并对后续内容进行展望:
- etcd存储引擎之主干框架(已完成):偏宏观视角下介绍 boltdb 的定位、架构、特性,通过几个核心流程浅探 boltdb 实现源码
- etcd存储引擎之存储设计(已完成):介绍 boltdb 存储模型、机制的设计实现,包含磁盘、内存两部分
- etcd存储引擎之b+树实现(本篇):介绍 b+ 树理论模型及 boltdb 实现案例,包括模型定义及 crud 流程梳理
- etcd存储引擎之事务实现(待填坑):介绍 boltdb 事务的执行模式及实现原理