理解矩阵乘法

大多数人在高中，或者大学低年级，都上过一门课《线性代数》。这门课其实是教矩阵。

刚学的时候，还蛮简单的，矩阵加法就是相同位置的数字加一下。

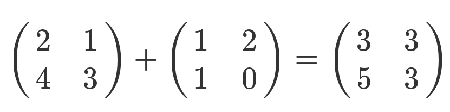
矩阵减法也类似。

矩阵乘以一个常数，就是所有位置都乘以这个数。

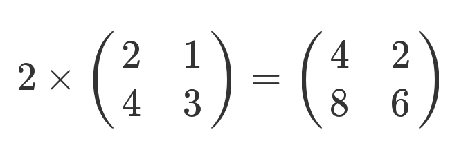
但是，等到矩阵乘以矩阵的时候，一切就不一样了。

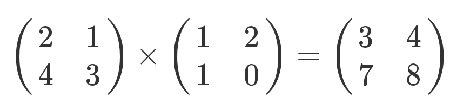
这个结果是怎么算出来的？

教科书告诉你，计算规则是，第一个矩阵第一行的每个数字（2和1），各自乘以第二个矩阵第一列对应位置的数字（1和1），然后将乘积相加（ 2 x 1 + 1 x 1），得到结果矩阵左上角的那个值3。

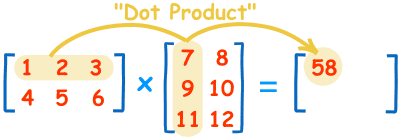
也就是说，结果矩阵第m行与第n列交叉位置的那个值，等于第一个矩阵第m行与第二个矩阵第n列，对应位置的每个值的乘积之和。

怎么会有这么奇怪的规则？

我一直没理解这个规则的含义，导致《线性代数》这门课就没学懂。研究生时发现，线性代数是向量计算的基础，很多重要的数学模型都要用到向量计算，所以我做不了复杂模型。这一直让我有点伤心。

前些日子，受到一篇文章的启发，我终于想通了，矩阵乘法到底是什么东西。关键就是一句话，矩阵的本质就是线性方程式，两者是一一对应关系。如果从线性方程式的角度，理解矩阵乘法就毫无难度。

下面是一组线性方程式。

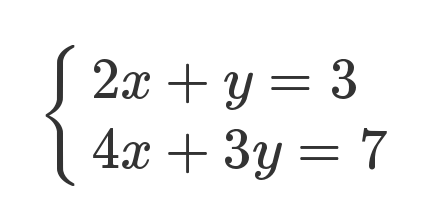
矩阵的最初目的，只是为线性方程组提供一个简写形式。

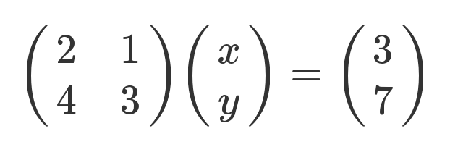
老实说，从上面这种写法，已经能看出矩阵乘法的规则了：系数矩阵第一行的2和1，各自与 x 和 y 的乘积之和，等于3。不过，这不算严格的证明，只是线性方程式转为矩阵的书写规则。

下面才是严格的证明。有三组未知数 x、y 和 t，其中 x 和 y 的关系如下。

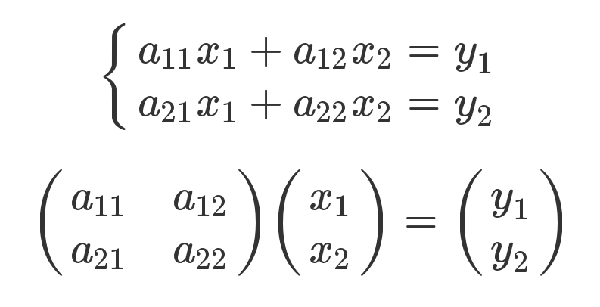
x 和 t 的关系如下。

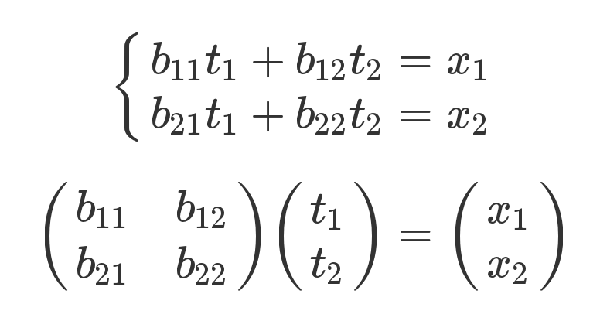
有了这两组方程式，就可以求 y 和 t 的关系。从矩阵来看，很显然，只要把第二个矩阵代入第一个矩阵即可。

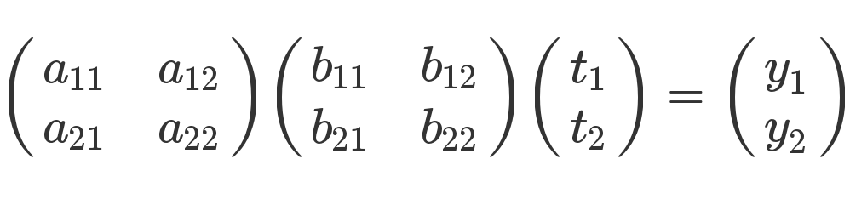
从方程式来看，也可以把第二个方程组代入第一个方程组。

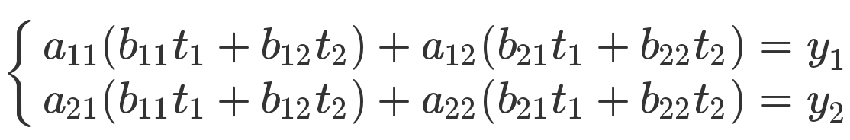
上面的方程组可以整理成下面的形式。

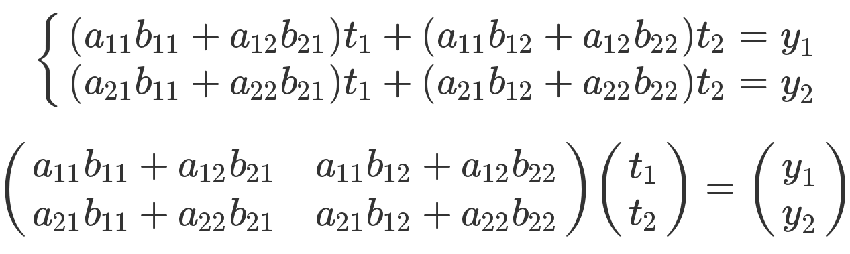
最后那个矩阵等式，与前面的矩阵等式一对照，就会得到下面的关系。

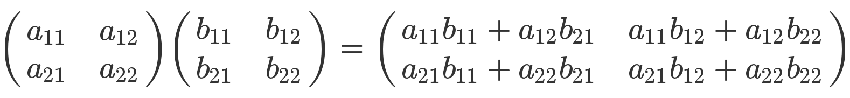
矩阵乘法的计算规则，从而得到证明。

=========================================

以下为广告部分。欢迎大家在我的网络日志投放广告。

[赞助商广告]

如果你想换工作，花五分钟，浏览一下 100offer，也许人生从此就会不同。

100offer 的目标是，只要你有2年以上的互联网工作经验（一线互联网公司更好），它就极有可能帮你拿到年薪 20W--80W 的 Offer。

它最近对514位用户的一份实证分析，有两点发现。

    （1）所有离职的工程师之中，BAT员工最受欢迎，新工作的薪酬通常可以翻番。
    （2）只有40%的程序员跳槽去了C轮、D轮和上市公司，其余60%都去了天使轮、A轮和B轮的公司，其中不乏资深的高级程序员。原因是这些创业公司刚刚起步、产品模式初步得到认可，上升空间大、技术人才需求量大、愿意给出较多的期权。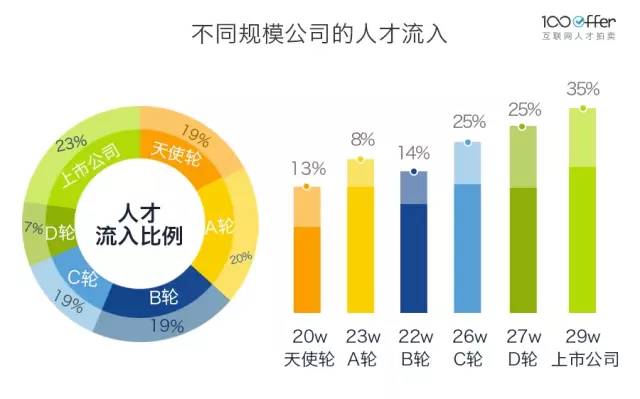

结合上面两点，年青程序员可以这样设计自己的职业生涯：

1、至少有一次大公司的成功工作经历。

所谓"成功"，是指参与过知名的产品开发或主力项目经验。这一般代表你已经具备：良好的代码规范、团队协作能力、与大牛一起工作的开阔眼界成熟的技术体系。

2、然后，加入一家高速发展的创业公司。

100offer 帮助你实现这条职业道路。