python实现逻辑回归的方法示例

本文实现的原理很简单，优化方法是用的梯度下降。后面有测试结果。

先来看看实现的示例代码：

    # coding=utf-8
    from math import exp

    import matplotlib.pyplot as plt
    import numpy as np
    from sklearn.datasets.samples_generator import make_blobs


    def sigmoid(num):
     '''

     :param num: 待计算的x
     :return: sigmoid之后的数值
     '''
     if type(num) == int or type(num) == float:
      return 1.0 / (1 + exp(-1 * num))
     else:
      raise ValueError, 'only int or float data can compute sigmoid'


    class logistic():
     def __init__(self, x, y): 
      if type(x) == type(y) == list:
       self.x = np.array(x)
       self.y = np.array(y)
      elif type(x) == type(y) == np.ndarray:
       self.x = x
       self.y = y
      else:
       raise ValueError, 'input data error'

     def sigmoid(self, x):
      '''

      :param x: 输入向量
      :return: 对输入向量整体进行simgoid计算后的向量结果
      '''
      s = np.frompyfunc(lambda x: sigmoid(x), 1, 1)
      return s(x)

     def train_with_punish(self, alpha, errors, punish=0.0001):
      '''

      :param alpha: alpha为学习速率
      :param errors: 误差小于多少时停止迭代的阈值
      :param punish: 惩罚系数
      :param times: 最大迭代次数
      :return:
      '''
      self.punish = punish
      dimension = self.x.shape[1]
      self.theta = np.random.random(dimension)
      compute_error = 100000000
      times = 0
      while compute_error > errors:
       res = np.dot(self.x, self.theta)
       delta = self.sigmoid(res) - self.y
       self.theta = self.theta - alpha * np.dot(self.x.T, delta) - punish * self.theta # 带惩罚的梯度下降方法
       compute_error = np.sum(delta)
       times += 1

     def predict(self, x):
      '''

      :param x: 给入新的未标注的向量
      :return: 按照计算出的参数返回判定的类别
      '''
      x = np.array(x)
      if self.sigmoid(np.dot(x, self.theta)) > 0.5:
       return 1
      else:
       return 0


    def test1():
     '''
     用来进行测试和画图，展现效果
     :return:
     '''
     x, y = make_blobs(n_samples=200, centers=2, n_features=2, random_state=0, center_box=(10, 20))
     x1 = []
     y1 = []
     x2 = []
     y2 = []
     for i in range(len(y)):
      if y[i] == 0:
       x1.append(x[i][0])
       y1.append(x[i][1])
      elif y[i] == 1:
       x2.append(x[i][0])
       y2.append(x[i][1])
     # 以上均为处理数据，生成出两类数据
     p = logistic(x, y)
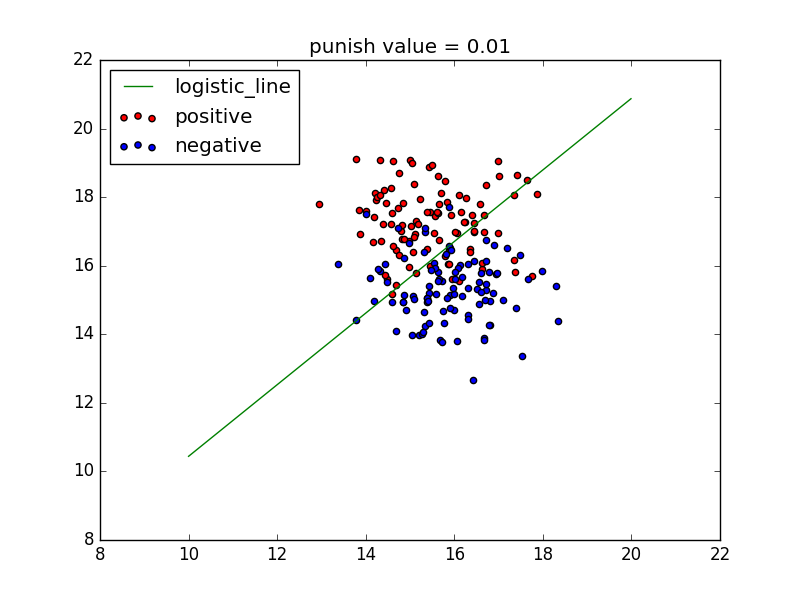
     p.train_with_punish(alpha=0.00001, errors=0.005, punish=0.01) # 步长是0.00001，最大允许误差是0.005，惩罚系数是0.01
     x_test = np.arange(10, 20, 0.01)
     y_test = (-1 * p.theta[0] / p.theta[1]) * x_test
     plt.plot(x_test, y_test, c='g', label='logistic_line')
     plt.scatter(x1, y1, c='r', label='positive')
     plt.scatter(x2, y2, c='b', label='negative')
     plt.legend(loc=2)
     plt.title('punish value = ' + p.punish.__str__())
     plt.show()


    if __name__ == '__main__':
     test1()

运行结果如下图

总结

以上就是这篇文章的全部内容了，希望本文的内容对大家的学习或者工作能带来一定的帮助，如果有疑问大家可以留言交流，谢谢大家对脚本之家的支持。