Python实现的数据结构与算法之基本搜索详解
本文实例讲述了Python实现的数据结构与算法之基本搜索。分享给大家供大家参考。具体分析如下:
一、顺序搜索
顺序搜索 是最简单直观的搜索方法:从列表开头到末尾,逐个比较待搜索项与列表中的项,直到找到目标项(搜索成功)或者 超出搜索范围 (搜索失败)。
根据列表中的项是否按顺序排列,可以将列表分为 无序列表 和 有序列表。对于 无序列表,超出搜索范围 是指越过列表的末尾;对于 有序列表,超过搜索范围 是指进入列表中大于目标项的区域(发生在目标项小于列表末尾项时)或者指越过列表的末尾(发生在目标项大于列表末尾项时)。
1、无序列表
在无序列表中进行顺序搜索的情况如图所示:

def sequentialSearch(items, target):
for item in items:
if item == target:
return True
return False2、有序列表
在有序列表中进行顺序搜索的情况如图所示:

def orderedSequentialSearch(items, target):
for item in items:
if item == target:
return True
elif item > target:
break
return False二、二分搜索
实际上,上述orderedSequentialSearch算法并没有很好地利用有序列表的特点。
二分搜索 充分利用了有序列表的优势,该算法的思路非常巧妙:在原列表中,将目标项(target)与列表中间项(middle)进行对比,如果target等于middle,则搜索成功;如果target小于middle,则在middle的左半列表中继续搜索;如果target大于middle,则在middle的右半列表中继续搜索。
在有序列表中进行二分搜索的情况如图所示:
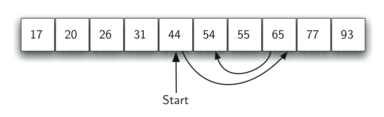
根据实现方式的不同,二分搜索算法可以分为迭代版本和递归版本两种:
1、迭代版本
def iterativeBinarySearch(items, target):
first = 0
last = len(items) - 1
while first <= last:
middle = (first + last) // 2
if target == items[middle]:
return True
elif target < items[middle]:
last = middle - 1
else:
first = middle + 1
return False2、递归版本
def recursiveBinarySearch(items, target):
if len(items) == 0:
return False
else:
middle = len(items) // 2
if target == items[middle]:
return True
elif target < items[middle]:
return recursiveBinarySearch(items[:middle], target)
else:
return recursiveBinarySearch(items[middle+1:], target)三、性能比较
上述搜索算法的时间复杂度如下所示:
搜索算法 时间复杂度
-----------------------------------
sequentialSearch O(n)
-----------------------------------
orderedSequentialSearch O(n)
-----------------------------------
iterativeBinarySearch O(log n)
-----------------------------------
recursiveBinarySearch O(log n)
-----------------------------------
in O(n)可以看出,二分搜索 的性能要优于 顺序搜索。
值得注意的是,Python的成员操作符 in 的时间复杂度是O(n),不难猜出,操作符 in 实际采用的是 顺序搜索 算法。
四、算法测试
#!/usr/bin/env python
# -*- coding: utf-8 -*-
def test_print(algorithm, listname, target):
print(' %d is%s in %s' % (target, '' if algorithm(eval(listname), target) else ' not', listname))
if __name__ == '__main__':
testlist = [1, 2, 32, 8, 17, 19, 42, 13, 0]
orderedlist = sorted(testlist)
print('sequentialSearch:')
test_print(sequentialSearch, 'testlist', 3)
test_print(sequentialSearch, 'testlist', 13)
print('orderedSequentialSearch:')
test_print(orderedSequentialSearch, 'orderedlist', 3)
test_print(orderedSequentialSearch, 'orderedlist', 13)
print('iterativeBinarySearch:')
test_print(iterativeBinarySearch, 'orderedlist', 3)
test_print(iterativeBinarySearch, 'orderedlist', 13)
print('recursiveBinarySearch:')
test_print(recursiveBinarySearch, 'orderedlist', 3)
test_print(recursiveBinarySearch, 'orderedlist', 13)运行结果:
$ python testbasicsearch.py
sequentialSearch:
3 is not in testlist
13 is in testlist
orderedSequentialSearch:
3 is not in orderedlist
13 is in orderedlist
iterativeBinarySearch:
3 is not in orderedlist
13 is in orderedlist
recursiveBinarySearch:
3 is not in orderedlist
13 is in orderedlist希望本文所述对大家的Python程序设计有所帮助。