程序的迭代
自然界中的某些"模型"是由不断重复的局部构成的整体,"迭代"则是人类对这些活动的认知中总结出来的模式。

迭代是重复反馈过程的活动,其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次"迭代",而每一次迭代得到的结果会作为下一次迭代的初始值。
线性的递归和迭代
首先考虑由下面表达式定义的阶乘运算:
n! = n * (n - 1) * (n - 2) ... * 3 * 2 * 1;
计算阶乘的方法有很多种,其中最简单的一种方式就是利用下述认知:
- 1的阶乘是1
- 对于任意一个大于1的整数n, n的阶乘是n与n-1的阶乘的乘积
我们将下述认知直接翻译成过程:
let factorial = (n) =>
n > 1 ? n * factorial(n - 1) : 1;
console.log(factorial(5)); //120
现在我们换另外一种思路,我们可以将计算阶乘n!看成是先乘起n和1,然后将得到的结果乘以n-1,而后再乘以n-2,这样依次下去直到达到1:
function factorial(n, acc = 1){
if (n <= 1) return acc;
return factorial(n - 1, n * acc);
}
console.log(factorial(5)); //120
抛开浮点数精度溢出的问题,前面一种递归方式当n比较大的时候,很快就堆栈溢出了,而后面一种迭代方式可以计算n很大的数。这是为什么呢?我们可以看一下两段代码计算时的堆栈----
factorial(5)
5 * factorial(4)
5 * (4 * factorial(3))
5 * (4 * (3 * factorial(2)))
5 * (4 * (3 * (2 * factorial(1))))
5 * (4 * (3 * (2 * (1))))
5 * (4 * (3 * (2)))
5 * (4 * (6))
5 * (24)
120
第一种递归的计算过程
factorial(5, 1)
factorial(4, 5);
factorial(3, 20);
factorial(2, 60);
factorial(1, 120);
120
第二种迭代的计算过程
上面看似两种类似的得出同样结果的计算过程,它们都采用与n成正比的步骤数去计算出n!,但是它们计算过程的"形状"不同,导致进展情况大不相同。
第一个计算过程中,整个表达式线性展开,直到最大深度,而后再逐步收缩,推导出计算结果。在展开阶段里,计算过程构造起一串推迟执行的操作链,并在收缩阶段实际执行出结果。这种类型的计算过程称为一个递归计算过程。要执行这种计算过程,解释器就需要维护其"轨迹"需要保存的信息量,这个长度随着n值而线性增长(意味着计算过程需要消耗较大的堆栈存储空间),这样的计算过程称为一个线性递归过程
与第一个计算过程不同,第二个计算过程中,并没有任何增长或收缩。对于任何一个n,在计算过程中的每一步在我们需要保存的"轨迹"里,所有的东西就是变量number、counter和max。我们称这种可以用固定数目的状态变量描述的过程为一个迭代计算过程。在计算n!的过程中,所需的计算步骤随着n线性增长,这种过程称为线性迭代过程。
利用babel编译输出,我们可以看一下针对线性递归过程和线性迭代过程,babel的不同处理方式:
"use strict";
var factorial = function factorial(n) {
return n > 1 ? n * factorial(n - 1) : 1;
};
console.log(factorial(5)); //120
对第一种线性递归过程的babel编译结果
"use strict";
function factorial(_x2) {
var _arguments = arguments;
var _again = true;
_function: while (_again) {
var n = _x2;
_again = false;
var acc = _arguments.length <= 1 || _arguments[1] === undefined ? 1 : _arguments[1];
if (n <= 1) return acc;
_arguments = [_x2 = n - 1, n * acc];
_again = true;
acc = undefined;
continue _function;
}
};
console.log(factorial(5)); //120
对第二种线性迭代过程的babel处理
上面可以看出,babel可以将线性迭代编译成循环来实现,从而去掉了语法形式上的递归(即函数调用自身),这也就是为什么babel编译的ES6线性迭代不会堆栈溢出。
注意:babel 6 因为其他bug的原因,暂时去掉了对线性迭代的优化,因此上面的代码是用 babel 5.8.35 进行编译的
因为上面的迭代过程在语法形式上也是递归,但它的特点是递归过程调用出现在函数的末尾,因此我们又称这个递归函数是尾递归( tail recursion )的。现代的许多编程语言的引擎会对这种情况做优化,类似于babel做的那样,不过目前v8引擎和其他的ES引擎本身并没有实现优化(尽管ES2015的标准中,语言规范规定引擎必须支持尾递归优化)。
由于JavaScript虽然可以用函数式这样的思路来构建模型,但是它本身也是有过程式语言的特征的,所以我们当然可以直接用循环:
let factorial = (n) => {
let ret = 1;
for(let i = 2; i <= n; i++){
ret *= i;
}
return ret;
}
console.log(factorial(5)); //120
绕了一圈,我们仿佛是回到了过程式编程的原点,是这样吗?事实上,因为阶乘问题足够简单,所以以任何一种思路都是差不多的。但随着我们要解决的问题复杂度的增加,两种思路的不同差异就能体现出来。
线性递归和线性迭代是最简单的形式,除了线性的模式常见的计算模式还有树形模式。
考虑斐波那契数列的计算,斐波那契数列中的每个数都是前两个数之和:
0, 1, 1, 2, 3, 5, 8, 13, 21, ...
一般来说,斐波那契数列由下面的规则定义:
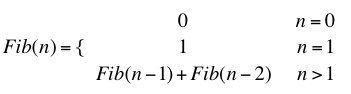
根据定义,我们很容易将它翻译为递归过程:
let fib = (n) => {
if(n === 0) return 0;
if(n === 1) return 1;
return fib(n - 1) + fib(n - 2);
};
console.log(fib(7)); //13
上述过程这样翻译虽然无比简单,但却是一种很糟糕的计算方法,它产生了大量的冗余计算,在优化它之前,我们先看一下它的计算过程:
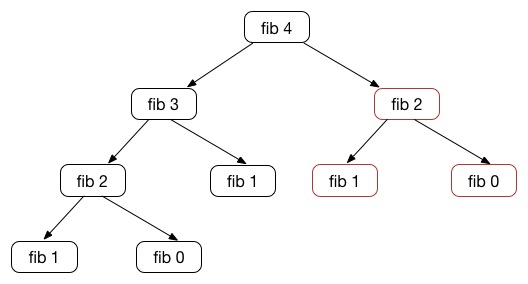
我们看到,其实这个计算过程的树形结构的每一个局部的左右是相似的,树形递归导致大量重复计算,比如上面的图示中当 n = 4时,fib(2)就被重复计算了2次,而随着n的增长,fib(2)的计算次数相对于n是指数级增长的。
我们可以改变思维方式,从n = 0和n = 1开始,规划出斐波那契数列的迭代计算过程,其基本方法是,令 a = fib(1) = 1, b = fib(0) = 0,然后反复地使用下面的变换规则:
[a, b] = [a + b, a];
在使用了n - 1次变换后,a、b将分别等于fib(n)和fib(n-1)。因此,我们得到下面的线性迭代过程:
let fib = (n, a = 1, b = 0) => {
if(n === 0) return b;
return fib(n - 1, a + b, a);
};
console.log(fib(7)); //13
这一次,计算模型让fib(n)的计算成为了线性增长,而不是指数增长,效率得到了极大的优化。同样,babel会将实际代码翻译成循环而不是使用递归,这消除了由于递归造成的空间线性增长。
"use strict";
var fib = function fib(_x5) {
var _arguments2 = arguments;
var _again2 = true;
_function2: while (_again2) {
var n = _x5;
var a = _arguments2.length <= 1 || _arguments2[1] === undefined ? 1 : _arguments2[1];
_again2 = false;
var b = _arguments2.length <= 2 || _arguments2[2] === undefined ? 0 : _arguments2[2];
if (n === 0) return b;
_arguments2 = [_x5 = n - 1, a + b, a];
_again2 = true;
a = b = undefined;
continue _function2;
}
};
console.log(fib(7)); //13
同样,我们也可以直接将它表达为循环:
let fib = (n) => {
if(n === 0) return 0;
let a = 1, b = 0;
for(let i = 2; i <= n; i++){
[a, b] = [a + b, a];
}
return a;
};
console.log(fib(7)); //13
在某些情况下树形递归的作用不可忽视,比如用JavaScript深度copy一个对象的时候,树形递归为我们提供了比较优雅的实现方式:
let deepCopy = (obj) => {
if(obj == null) return obj;
let copyed = {};
for(let key in obj){
if(typeof obj[key] === "object"){
copyed[key] = deepCopy(obj[key]);
}else{
copyed[key] = obj[key];
}
}
return copyed;
};
let a = {a:{x:1, y:2}, b:3, c:function(){}};
let b = deepCopy(a);
console.log(b.a.x); //1
b.a.y = 3;
console.log(b.a.y, a.a.y); //3, 2
迭代的优雅之处还有有时它仅仅只是描述问题本身而不需要关心详细解决步骤就能将问题优雅解决。再举一个例子:
使用迭代实现快速排序:
function qsort(arr){
if(arr.length <= 1) return arr;
var c = arr[0], rest = arr.slice(1);
return qsort(rest.filter(item => item < c))
.concat([c]).concat(qsort(rest.filter(item => item >= c)));
}
总结
迭代是一种常用的编程模型,使用它能够以简单优雅的方式得到我们想要的结果。递归形式的迭代有调用堆栈增长的弊端,当问题规模较大时很容易导致堆栈溢出。不过,现代编程语言通常支持尾递归优化,能够避免尾部调用时的递归堆栈溢出。ES的引擎目前还不支持尾递归优化,但是我们可以用Babel来编译(Babel 6暂时不支持)。